Python Coding Challenge - What is the maximum sum of a subarray of a given array?
(Python コーディングチャレンジ [決められた長さのサブセットのうち合計値が最大のものはどれ?]編)
(Python コーディングチャレンジ [決められた長さのサブセットのうち合計値が最大のものはどれ?]編)
Sliding window approach (スライディングウィンドウアプローチ) を利用すればそれほど難しい問題ではありません。ですが、より効率の良いアルゴリズムを考えましょう!
問題:
int 値を要素とする配列 nums と int 値 k が与えられます。配列 nums において連続する k 個の要素の合計が最も高いものを探し、その合計値を返してください。
例1:
nums = [100, 200, 300, 400]
k = 2
k = 2
# 出力: 700
例1の解説:
サイズが 2 のスライディングウィンドウを考えます。つまり max(100+200, 200+300, 300+400) = 700 となります。
例2:
nums = [1, 4, 2, 10, 23, 3, 1, 0, 20]
k = 4
k = 4
# 出力: 39
例2の解説:
サイズが 4 のスライディングウィンドウを考えます。つまり max(1+4+2+10, 4+2+10+23, 2+10+23+3, 10+23+3+1, 23+3+1+0, 3+1+0+20) = 39 となります。
また関数定義は以下のような形です (同じである必要はありません):
def maxsumk(self, nums: list[int], k: int) -> int:
...
...
考え方:
まず最初に通常の sliding window approach を採用して実装します。続けてより効率の良い実装方法を考えましょう。
Brute force method
(通常の sliding window approach: ちょっと力ずく戦法)
まず最初に最大合計値を保存しておくための変数 max_sum を「マイナス無限大」に設定しておきます。これは nums の要素がマイナスである可能性もあることを考慮したものです。
続けて nums をスキャンしていく i を定義します。i の取り得る範囲は 0 から len(nums)-k までになります。そしてもう1つのポインタ j で i から長さ k のサブセットをループしながら各要素の合計を求め curr_sum 変数に保存します。
最終的に現在の最大合計値 max_sum と今回のサブセットの合計値 curr_sum の大きい方の値を max_sum に保存します。全てのサブセットの検証が終了した時点で max_sum 変数の値を返します。
「通常の sliding window approach: ちょっと力ずく戦法」の実装例:
def maxsumk(nums: list[int], k: int) -> int:
max_sum = float('-Infinity')
for i in range(len(nums) - k + 1):
curr_sum = 0
for j in range(i, i + k):
curr_sum += nums[j]
max_sum = max(max_sum, curr_sum)
return max_sum
if __name__ == '__main__':
nums = [80, -50, 90, 100]
k = 2
print(maxsumk(nums, k))
max_sum = float('-Infinity')
for i in range(len(nums) - k + 1):
curr_sum = 0
for j in range(i, i + k):
curr_sum += nums[j]
max_sum = max(max_sum, curr_sum)
return max_sum
if __name__ == '__main__':
nums = [80, -50, 90, 100]
k = 2
print(maxsumk(nums, k))
# 出力: 190
Complexity Analysis
(アルゴリズム解析 - 実行時間解析)
配列の長さを n とすると、外側のループは n 回、内側のループは k 回実行することになります。よって全体の時間計算量 (time complexity) は O(nk) になります。この場合、k が定数であれば O(n) になりますが、k が n の倍数 (分数倍の場合も含みます)、すなわち k = f * n と表せる場合は O(n * f * n) -> O(n²) となります。
要素数を 4 から 500 まで変化させ、その都度の取り出すサブセットの長さを要素数の半分に設定した場合に、それぞれの要素数で各要素が 3 から 10 までの値を取るランダムな配列を作成する 100 回の試行を行なった場合の実行時間計測グラフは次のようになります。まさに O(n²) であることが分かります:
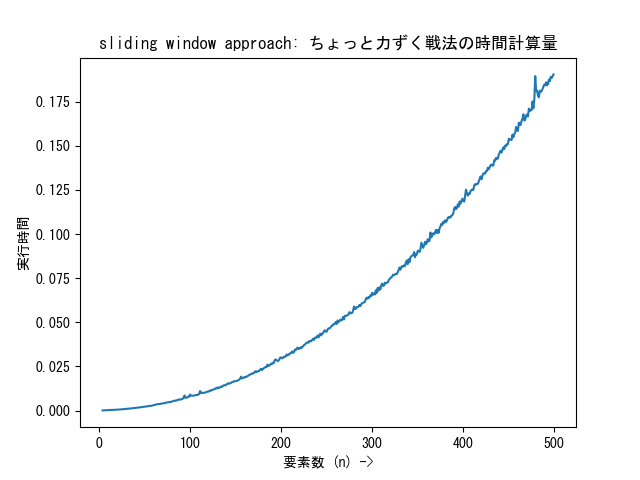
「通常の sliding window approach: ちょっと力ずく戦法」の実行時間計測グラフ
Efficient method
(効率的な sliding window approach)
外側のループを要素数 n 回分実行する必要があることには変更の余地がありませんが、内側のループをより効率的に実行することは可能です。
例えば次の配列が与えられたとします:
nums = [1, 4, 2, 10, 23, 3, 1, 0, 20]
この時 k = 4 が与えられた場合の各サブセットは次のような組み合わせになります:
1+4+2+10, 4+2+10+23, 2+10+23+3, 10+23+3+1, 23+3+1+0, 3+1+0+20
それぞれのサブセットをよく見てください。内側のループ1回の処理につき k 回の足し算を行っています。つまりこの例では4回です。しかし、最初のサブセットを除いて、2つ目以降のサブセットの前半3つの足し算はすでに前回のループで計算済みのものですね。
内側のループの先頭のインデックス番号は外側のループ i で押さえています。ですから、この内側のループの足し算は、前回のループの合計から nums[i - 1] を引き nums[i + k - 1] を足したもの、と等しくなります。4回全ての足し算を行う必要があるのは最初のサブセットのみ、ということです。
この考え方によって、内側のループの実行回数は k 回から 2 回へと減少します。また、k が変化したとしても実行回数は常に 2 回に固定されています。よってこの場合の内側のループの時間計算量は O(k) から O(1) に減少することになります:
「効率的な sliding window approach」の実装例:
def maxsumk(nums: list[int], k: int) -> int:
max_sum = float('-Infinity')
curr_sum = 0
for j in range(k): # 最初の項目は全ての足し算を行う
curr_sum += nums[j]
max_sum = curr_sum
curr_sum = curr_sum - nums[i - 1] + nums[i + k - 1]
max_sum = max(max_sum, curr_sum)
return max_sum
if __name__ == '__main__':
nums = [80, -50, 90, 100]
k = 2
print(maxsumk(nums, k))
max_sum = float('-Infinity')
curr_sum = 0
for j in range(k): # 最初の項目は全ての足し算を行う
curr_sum += nums[j]
max_sum = curr_sum
# 2番目以降の項目は前回の項目から nums[i - 1] を引き nums[i + k - 1] を足す
for i in range(1, len(nums) - k + 1):curr_sum = curr_sum - nums[i - 1] + nums[i + k - 1]
max_sum = max(max_sum, curr_sum)
return max_sum
if __name__ == '__main__':
nums = [80, -50, 90, 100]
k = 2
print(maxsumk(nums, k))
# 出力: 190
Complexity Analysis
(アルゴリズム解析 - 実行時間解析)
外側のループの時間計算量 (time complexity) は O(n) のままですが、内側のループは O(1) となります。よってプログラム全体では O(n) となります。
条件は変えずにこのアルゴリズムで試行を行なった場合の実行時間計測グラフは次のようになります。まさに O(n) ですね:
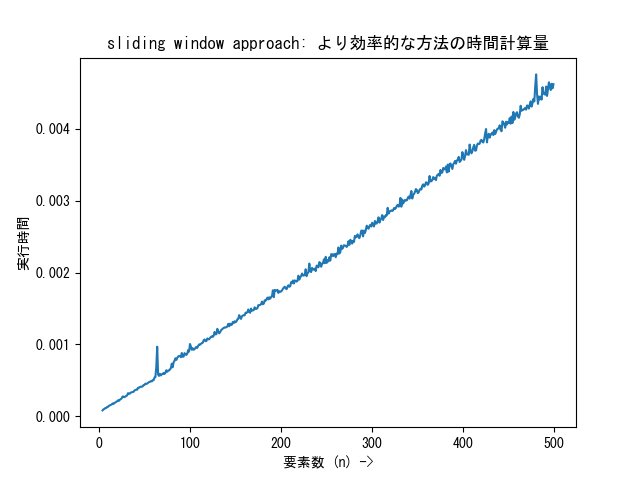
「sliding window approach: より効率的な方法」の実行時間計測グラフ

