RSSフィードを購読
Python Coding Challenge - How will you reconstruct the itinerary from tickets?
(Python コーディングチャレンジ [渡された航空券から旅程表を作り直そう！] 編)
(Python コーディングチャレンジ [渡された航空券から旅程表を作り直そう！] 編)
文章問題をグラフとしてモデル化する練習です。グラフに対して DFS を適用し如何に解を導き出すか、早速取り組んでみましょう！
問題：
あなたは旅行会社で世界中のあちらこちらを観光して回る相談をして航空券を手配してもらいました。しかしその旅行会社の担当者は旅程表をあなたに渡し忘れたまま休暇に入ってしまいました。あなたが知っているのは「旅行は JFK 国際空港から始まる」ということだけです。渡された航空券から「旅程表」を作り出すプログラムを記述してください。旅程を組む際の条件は以下の通りです:
1枚の航空券には「出発地 - 目的地」が IATA の３文字のコードで記されています。例えば、ジョン・F・ケネディ国際空港であれば 'JFK'、成田国際空港であれば 'NRT'、台湾桃園国際空港であれば 'TPE' といった具合です。
もしある出発地から複数の目的地が設定されている場合、目的地のアルファベット順に探索しなければいけません。例えば、JFK - NRT と JFK - TPE の航空券がある場合、NRT と TPE をアルファベット順で並べると NRT が先で TPE が後になりますから、JFK からは NRT を先に探索することになります。また、同じ「出発地 - 目的地」の航空券が複数含まれている可能性があります。
全ての航空券を使わなければいけません。ただしそれぞれの航空券は１回だけ使用します。
例 1:
渡される航空券: [['NRT', 'KBP'], ['JFK', 'NRT'], ['WAW', 'NRT'], ['KBP', 'WAW']]
# 出力: ['JFK', 'NRT', 'KBP', 'WAW', 'NRT']
例 1 の解説：
出発地は常に JFK です。JFK からの目的地は NRT、NRT からの目的地は KBP ...、ですから出力のようになります。
例 2:
渡される航空券: [['NRT', 'TPE'], ['NRT', 'KBP'], ['JFK', 'NRT'], ['WAW', 'NRT'], ['KBP', 'WAW']]
# 出力: ['JFK', 'NRT', 'KBP', 'WAW', 'NRT', 'TPE']
例 2 の解説：
出発地は常に JFK です。JFK からの目的地は NRT、NRT からの目的地は KBP と TPE ですが、アルファベット順に KBP を先に探索しますから出力の順番になります。
また関数定義は以下のような形です (同じである必要はありません):
def find_itinerary(tickets: list[list[str]]) -> list[str]:
...
...
作成したプログラムは以下のテストをパスする必要があります:
import unittest
class TestFindItinerary(unittest.TestCase):
def test_1(self):
tickets = [['NRT', 'KBP'], ['JFK', 'NRT'], ['WAW', 'NRT'], ['KBP', 'WAW'], ['NRT', 'TPE']]
res = find_itinerary(tickets)
self.assertEqual(res, ['JFK', 'NRT', 'KBP', 'WAW', 'NRT', 'TPE'])
def test_2(self):
tickets = [['LHR', 'FRA'],['JFK', 'LHR'],['FRA', 'NRT'],['NRT', 'TPE'],['TPE', 'NRT'], ['NRT', 'YVR'], ['YVR', 'LAX'], ['LAX', 'NRT']]
res = find_itinerary(tickets)
self.assertEqual(res, ['JFK', 'LHR', 'FRA', 'NRT', 'TPE', 'NRT', 'YVR', 'LAX', 'NRT'])
def test_3(self):
tickets = [['JFK','SIN'],['JFK','BOM'],['SIN','BOM'],['BOM','JFK'],['BOM', 'SIN']]
res = find_itinerary(tickets)
self.assertEqual(res, ['JFK', 'BOM', 'JFK', 'SIN', 'BOM', 'SIN'])
def test_4(self):
tickets = [['JFK','BOM'],['BOM','SIN'],['SIN','NRT']]
res = find_itinerary(tickets)
self.assertEqual(res, ['JFK', 'BOM', 'SIN', 'NRT'])
def test_5(self):
tickets = [['EZE', 'TIA'],['EZE', 'HBA'],['AXA', 'TIA'],['JFK', 'AXA'],['ANU', 'JFK'],['ADL', 'ANU'],['TIA', 'AUA'],['ANU', 'AUA'],['ADL', 'EZE'],['ADL', 'EZE'],['EZE', 'ADL'],['AXA', 'EZE'],['AUA', 'AXA'],['JFK', 'AXA'],['AXA', 'AUA'],['AUA', 'ADL'],['ANU', 'EZE'],['TIA', 'ADL'],['EZE', 'ANU'],['AUA', 'ANU']]
res = find_itinerary(tickets)
self.assertEqual(res, ['JFK', 'AXA', 'AUA', 'ADL', 'ANU', 'AUA', 'ANU', 'EZE', 'ADL', 'EZE', 'ANU', 'JFK', 'AXA', 'EZE', 'TIA', 'AUA', 'AXA', 'TIA', 'ADL', 'EZE', 'HBA'])
def test_6(self):
tickets = [['JFK','NRT'],['NRT','LAX'],['NRT','TPE'], ['TPE', 'HNL'], ['HNL', 'NRT'], ['TPE', 'YVR'], ['YVR', 'HNL'], ['HNL', 'TPE']]
res = find_itinerary(tickets)
self.assertEqual(res, ['JFK', 'NRT', 'TPE', 'HNL', 'TPE', 'YVR', 'HNL', 'NRT', 'LAX'])
class TestFindItinerary(unittest.TestCase):
def test_1(self):
tickets = [['NRT', 'KBP'], ['JFK', 'NRT'], ['WAW', 'NRT'], ['KBP', 'WAW'], ['NRT', 'TPE']]
res = find_itinerary(tickets)
self.assertEqual(res, ['JFK', 'NRT', 'KBP', 'WAW', 'NRT', 'TPE'])
def test_2(self):
tickets = [['LHR', 'FRA'],['JFK', 'LHR'],['FRA', 'NRT'],['NRT', 'TPE'],['TPE', 'NRT'], ['NRT', 'YVR'], ['YVR', 'LAX'], ['LAX', 'NRT']]
res = find_itinerary(tickets)
self.assertEqual(res, ['JFK', 'LHR', 'FRA', 'NRT', 'TPE', 'NRT', 'YVR', 'LAX', 'NRT'])
def test_3(self):
tickets = [['JFK','SIN'],['JFK','BOM'],['SIN','BOM'],['BOM','JFK'],['BOM', 'SIN']]
res = find_itinerary(tickets)
self.assertEqual(res, ['JFK', 'BOM', 'JFK', 'SIN', 'BOM', 'SIN'])
def test_4(self):
tickets = [['JFK','BOM'],['BOM','SIN'],['SIN','NRT']]
res = find_itinerary(tickets)
self.assertEqual(res, ['JFK', 'BOM', 'SIN', 'NRT'])
def test_5(self):
tickets = [['EZE', 'TIA'],['EZE', 'HBA'],['AXA', 'TIA'],['JFK', 'AXA'],['ANU', 'JFK'],['ADL', 'ANU'],['TIA', 'AUA'],['ANU', 'AUA'],['ADL', 'EZE'],['ADL', 'EZE'],['EZE', 'ADL'],['AXA', 'EZE'],['AUA', 'AXA'],['JFK', 'AXA'],['AXA', 'AUA'],['AUA', 'ADL'],['ANU', 'EZE'],['TIA', 'ADL'],['EZE', 'ANU'],['AUA', 'ANU']]
res = find_itinerary(tickets)
self.assertEqual(res, ['JFK', 'AXA', 'AUA', 'ADL', 'ANU', 'AUA', 'ANU', 'EZE', 'ADL', 'EZE', 'ANU', 'JFK', 'AXA', 'EZE', 'TIA', 'AUA', 'AXA', 'TIA', 'ADL', 'EZE', 'HBA'])
def test_6(self):
tickets = [['JFK','NRT'],['NRT','LAX'],['NRT','TPE'], ['TPE', 'HNL'], ['HNL', 'NRT'], ['TPE', 'YVR'], ['YVR', 'HNL'], ['HNL', 'TPE']]
res = find_itinerary(tickets)
self.assertEqual(res, ['JFK', 'NRT', 'TPE', 'HNL', 'TPE', 'YVR', 'HNL', 'NRT', 'LAX'])
考え方:
与えられるデータは旅行券のリストで、１枚の旅行券は「出発地 - 目的地」のペアで成り立っています。つまり旅行券はグラフを構成する「有向 edge (directional edge)」であり、それぞれの空港をノード (node / vertex) と捉えることができる、ということです。ですから、現在の旅行券の目的地が次の旅行券の出発地になるわけです。ということは、与えられた旅行券リストで表現されている graph を DFS アルゴリズムを利用して走査/探索 (traverse) する必要があることを示しています。
前回の「Python coding challenge - DFS (Depth First Search) Traversal of Graphs and Trees: 『深さ優先探索』によるグラフ及びツリーの探索」で学習したように、DFS による探索順序は一意に決まるわけではありません。しかしこの問題では「複数の目的地がある場合はアルファベット順に探索しなければならない」という制約がついていますから、走査する順番が一意に決まることになります。
この制約を満たすこと自体は難しいことではありません。渡されてきた tickets リストを目的地のアルファベット順に並べ替えてしまえばいいだけです。しかし渡されてくる tickets リストの各要素は２要素からなるリストであり、目的地データはそのリストの２番目の要素です。さてどうしましょう？
方法はいろいろ考えられますが、もっとも効率的な方法は list の sort() を利用し key 属性として並べ替えの基準となる要素を返す関数を指定することでしょう。そのための関数を定義することもできますが、今回は lambda 関数を利用したいと思います:
tickets.sort(key=lambda x: x[1])
また同じく問題の条件 2 には「同じ『出発地 - 目的地』の航空券が複数含まれている可能性がある」ということが記されています。この条件が学習した基本的な DFS の実装に与える影響は何でしょうか？「基本的な実装」では既に処理したノードを visited リストに加えていき「訪問の重複」が起きないようにしていました。しかし今回の問題では一度訪れたノードを再度訪れることが許されていなければなりません。しかし問題の条件 3 にあるように「それぞれの航空券は１回だけ使用できる」わけですから、この区別もできるようにする必要があります。
ということで、これらの条件を満たすために今回は visited リストを利用せず、「使用した」航空券自体を tickets リストから「削除」してしまうことにします。そうすることで「使用の重複」を避けられると同時に、「同じ『出発地 - 目的地』ペア」の航空券を個別に利用できるようになります。
あと１つ「基本的な実装」からの変更点があります。「基本的な実装」ではノードを探索するたびにそのノードを出力していました。しかし今回は条件を満たすたびに内部変数 path に保存し、最後に一気に出力することにします。この処理が必要な理由はおいおい理解できてくると思います。
さて、簡単な例を使って処理の流れを確認してみましょう。与えられる tickets は以下の通りとします:
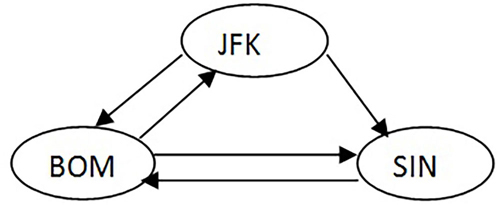
tickets = [['JFK','SIN'],['JFK','BOM'],['SIN','BOM'],['BOM','JFK'],['BOM', 'SIN']]
これは次のグラフを表現しています:
Tickets graph
- Shyamkant Limaye (2021). Python Quick Interview Guide. BPB Publications -
最初にやるべきことは、受け取った tickets リストを基にグラフを表現する隣接リスト (adjacency list) を作成することです。この隣接リストは dictionary として実装し、key は出発地の空港コード、value は目的地の空港コードを要素とする list です。また、存在しない key に対して value を append しても例外が発生しないように、通常の dictionary の代わりに collections モジュールの defaultdict クラスを利用します。作成した隣接リストは以下のようになります:
BOM:['JFK', 'SIN']
JFK:['BOM', 'SIN']
SIN: ['BOM']
JFK:['BOM', 'SIN']
SIN: ['BOM']
続いてグラフの横断/走査処理 (traversing) を行います。ここでの満たすべき条件は「全ての航空券を使い切ること」と「１枚の航空券は１回だけ使用する」ことです。今回は走査処理を行うために再帰関数 dfs を実装します。この recursive function は「出発地コード」を引数として受け取り、値は返しません。処理したノードは path 変数へ append していきます。もし「出発地コード」から「外向きの edge (outgoing edge)」が出ていれば、すなわち「目的地」があれば、その「目的地コード」を取り出すと同時にその edge を削除します。こうすることで同じ航空券の「再使用」を防止します。そして取り出した「目的地コード」を引数として再度自分自身を呼び出します。この再帰処理の base case (再帰処理が終了する条件) は、渡された「出発地」から行くべき「目的地」がない、すなわち、出発地 key の value である目的地 list が空、である時です。
再帰処理では「１つの枝」を深さ方向に探索していき、その枝の末端まで辿り着いたところでその時点のノードを path リストに append していきます。つまりこの path リストに追加されていく「出発地コード」はそこから先に行くべき「目的地」がない「最終目的地」から「最初の出発地」である JFK に向かって逆順に並ぶことになります。DFS における用語でいえば、枝の末端のノードからルートノードに向けて append していく、ということです。
この append の方法には２つの実装方法が考えられます。逆順のリストができてしまうことが嫌なのであれば、path リストに追加する際に path.insert(0, s) という構文を利用すればリストの先頭に追加していくことができますから、最終的な path リスト内の要素の順番は訪問すべき場所の順番そのものになっています。しかし append を実行するたびにこの構文を実行するのはあまり効率が良いとは言えません。そこで今回は、全ての処理の最後に path リストの内容をリバースする処理を実行することにします。
この例における処理の流れと各変数の値を列挙すると次のようになります:
出発地 (start) 隣接リスト (adjacent list) 目的地 (next)
JFK BOM:[JFK, SIN], JFK:[BOM, SIN], SIN:[BOM] BOM
BOM BOM:[JFK, SIN], JFK:[SIN], SIN:[BOM] JFK
JFK BOM:[SIN], JFK:[SIN], SIN:[BOM] SIN
SIN BOM:[SIN], JFK:[], SIN:[BOM] BOM
BOM BOM:[SIN], JFK:[], SIN:[] SIN
SIN BOM:[], JFK:[], SIN:[]
JFK BOM:[JFK, SIN], JFK:[BOM, SIN], SIN:[BOM] BOM
BOM BOM:[JFK, SIN], JFK:[SIN], SIN:[BOM] JFK
JFK BOM:[SIN], JFK:[SIN], SIN:[BOM] SIN
SIN BOM:[SIN], JFK:[], SIN:[BOM] BOM
BOM BOM:[SIN], JFK:[], SIN:[] SIN
SIN BOM:[], JFK:[], SIN:[]
最後の行では全ての出発地から outgoing edges が出ていません。すなわち旅行券はすべて使用し、全ての目的地を訪問しましたからプログラムが終了します。よって旅程表は次のように作成されます:
['JFK', 'BOM', 'JFK', 'SIN', 'BOM', 'SIN']
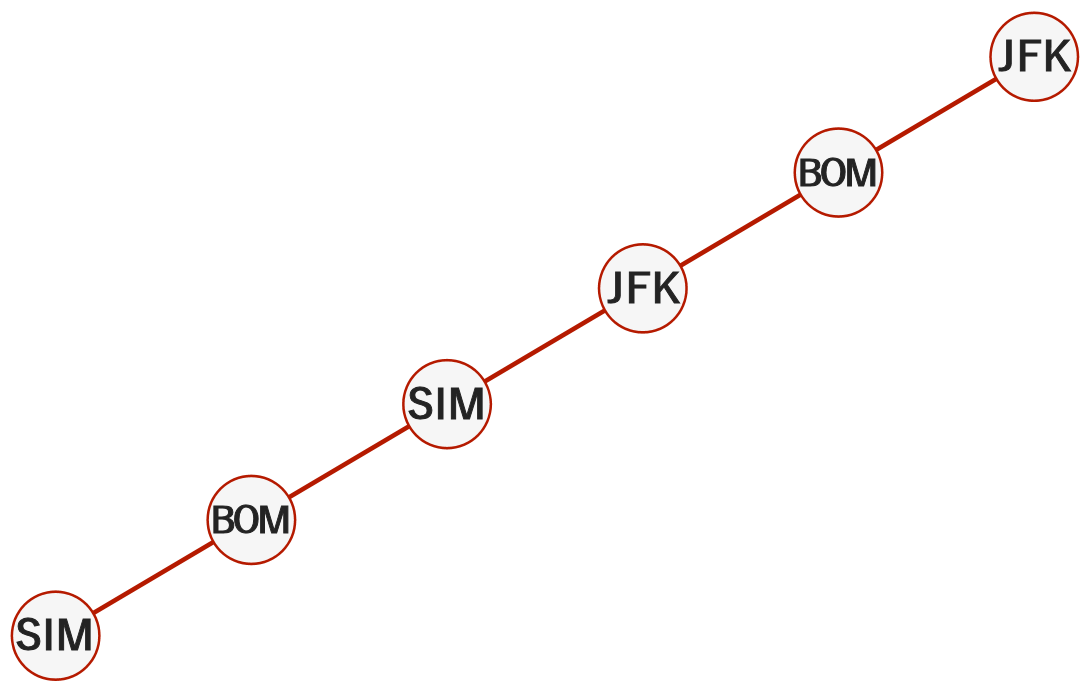
この DFS シリーズの始めの回で、「グラフに対して DFS を適用するということは『ツリーデータ構造を形成している』ということにほかならない」という話をしました。今回のプログラムにおいて作成しているツリー構造は以下のようになります:
Graph に対して DFS を適用して作成される tree
今回の考え方において「なぜ訪れる出発地を前から順番に path リストに append せずに最終目的地から逆順に append しているのだろう？」と感じた方はいるでしょうか？グラフを見ているだけでは分かり辛いですが、グラフに対して DFS を適用することで形成しているツリーを考えてみることでこの答えを導き出すことができます。
上の例のように「形成されるツリー」に分岐がない場合は最初の訪問地から順番に path リストに append しても問題はありません。しかし unittest の test_6 で表現しているグラフに対して DFS を適用した結果形成されるツリーには分岐が含まれます。
このテスト 6 の tickets リストから作成したグラフを表現する隣接リストは次のようになります:
'TPE': ['HNL', 'YVR'],
'YVR': ['HNL'],
'NRT': ['LAX', 'TPE'],
'JFK': ['NRT'],
'HNL': ['NRT', 'TPE'],
'YVR': ['HNL'],
'NRT': ['LAX', 'TPE'],
'JFK': ['NRT'],
'HNL': ['NRT', 'TPE'],
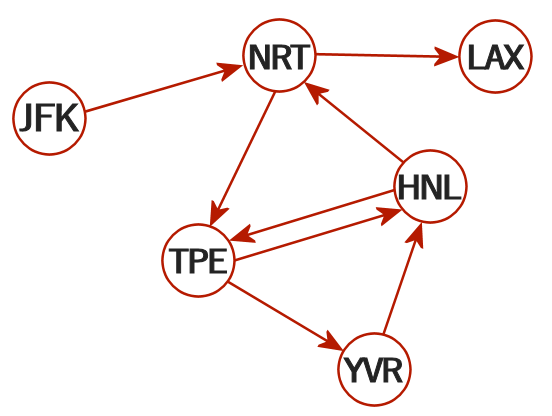
このグラフを図で表すと次のようになります:
test_6 が表現しているグラフ
そしてこのグラフを DFS アルゴリズムで探索することで暗黙のうちに形成しているツリーは次のようになります:
test_6 が表現しているグラフに DFS アルゴリズムを適用して形成している探索ツリー
今回の問題では「目的地はアルファベット順に探索しなければならない」という条件が付いています。ある出発地からの訪問地が複数あり、アルファベット順に先に探索した訪問地からその先の訪問地が存在しない場合、つまりツリーの末端に到達してしまった場合、その場所は本来であれば分岐した元の出発地からは後で訪問しなければならない目的地であることを示しています。ですから、探索した順番に path リストに append していってしまうとこの状況に対処できない、ということです。そのために「分岐した元の出発地」から「後で訪問すべき目的地」を見つけた段階で path リストに append し、そこから「元の出発地」にツリーを戻りながら経由地を追加していく、ことが必要になります。
プログラム実装例：
from collections import defaultdict
def find_itinerary(tickets: list[list[str]]) -> list[str]:
tickets.sort(key=lambda x: x[1]) # 目的地のアルファベット順にソート
dest = defaultdict(list) # グラフを表現する隣接リスト
path: list[str] = [] # 旅程リスト
start = 'JFK'
for source, destination in tickets: # 隣接リストの作成
dest[source].append(destination)
def dfs(start: str):
while dest[start]:
next = dest[start].pop(0)
dfs(next)
path.append(start) # 最終目的地から最初の出発地 (JFK) に向けてリストに追加
dfs(start)
return path[::-1] # 訪問順に並べるためにリバース処理を行なう
def find_itinerary(tickets: list[list[str]]) -> list[str]:
tickets.sort(key=lambda x: x[1]) # 目的地のアルファベット順にソート
dest = defaultdict(list) # グラフを表現する隣接リスト
path: list[str] = [] # 旅程リスト
start = 'JFK'
for source, destination in tickets: # 隣接リストの作成
dest[source].append(destination)
def dfs(start: str):
while dest[start]:
next = dest[start].pop(0)
dfs(next)
path.append(start) # 最終目的地から最初の出発地 (JFK) に向けてリストに追加
dfs(start)
return path[::-1] # 訪問順に並べるためにリバース処理を行なう
Complexity Analysis
(アルゴリズム解析)
Time complexity (実行計算時間):
Tickets の数が n 枚の場合再帰関数 dfs() を n + 1 回呼び出します。よって O(n) です。
Space complexity (実行メモリ要求量):
訪問先を保存しておくための list が必要です。よって O(n) です。