RSSフィードを購読
Python Coding Challenge - How will you find the path sum in a binary tree?
(Python コーディングチャレンジ [パスを構成するノードの value の合計値が target と同じものを見つけよう！] 編)
(Python コーディングチャレンジ [パスを構成するノードの value の合計値が target と同じものを見つけよう！] 編)
この問題も DFS アルゴリズムを利用する問題のバリエーションの１つです。ルートノードから全てのリーフノードに至る path を列挙し、それぞれの path を構成するノードの value 値の合計をキープ、比較するものです。
問題：
バイナリツリーが渡されます。このバイナリツリーを構成する各ノードの value は int 値です。この時、ルートノードからリーフノードに至る paths の中に、その path を構成するノードの value の合計値が与えられる target と等しいものがあるか否かを返すプログラムを記述してください。合計値が target と等しいものが含まれる場合は True、含まれない場合は False を返します。
例：
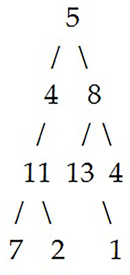
下図のバイナリツリーと target として 22 が渡されたとします:
(例) 渡されるバイナリツリー
- Shyamkant Limaye (2021). Python Quick Interview Guide. BPB Publications -
与えられる引数: root, 22
# 出力: True
例の解説：
与えられたバイナリツリーに含まれるパス 5-4-11-2 の合計値は 22 であり、指定された target と同じです。よって True を返します。
また関数定義は以下のような形です (同じである必要はありません):
from typing import Optional
def has_path_sum(root: Optional[TreeNode], sum: int) -> bool:
...
def has_path_sum(root: Optional[TreeNode], sum: int) -> bool:
...
また TreeNode クラスは「Python coding challenge の前準備: Basics of Graph Theory Part.3 - Representation and Manipulation of Trees (グラフ理論の基礎総復習 その３ - ツリーの表現と操作)」で定義した次のクラスを利用します:
from typing import Optional, Any
class TreeNode:
def __init__(self, v: Any):
self.val = v
self.left: Optional[TreeNode] = None
self.right: Optional[TreeNode] = None
class TreeNode:
def __init__(self, v: Any):
self.val = v
self.left: Optional[TreeNode] = None
self.right: Optional[TreeNode] = None
作成したプログラムは以下のテストをパスする必要があります:
import unittest
def make_tree(arr: list[Optional[int]], root: Optional[TreeNode] = None, index: int = 0) -> Optional[TreeNode]:
if index < len(arr):
root = TreeNode(arr[index])
root.left = make_tree(arr, root.left, index * 2 + 1)
root.right = make_tree(arr, root.right, index * 2 + 2)
return root
class TestHasPathSum(unittest.TestCase):
def setUp(self):
arr = [5, 4, 8, 11, None, 13, 4, 7, 2, None, None, None, 1, None, None]
self.root = make_tree(arr)
def test_1(self):
res = has_path_sum(self.root, 27)
self.assertTrue(res)
def test_2(self):
res = has_path_sum(self.root, 22)
self.assertTrue(res)
def test_3(self):
res = has_path_sum(self.root, 11)
self.assertFalse(res)
def test_4(self):
res = has_path_sum(self.root, 17)
self.assertTrue(res)
def make_tree(arr: list[Optional[int]], root: Optional[TreeNode] = None, index: int = 0) -> Optional[TreeNode]:
if index < len(arr):
root = TreeNode(arr[index])
root.left = make_tree(arr, root.left, index * 2 + 1)
root.right = make_tree(arr, root.right, index * 2 + 2)
return root
class TestHasPathSum(unittest.TestCase):
def setUp(self):
arr = [5, 4, 8, 11, None, 13, 4, 7, 2, None, None, None, 1, None, None]
self.root = make_tree(arr)
def test_1(self):
res = has_path_sum(self.root, 27)
self.assertTrue(res)
def test_2(self):
res = has_path_sum(self.root, 22)
self.assertTrue(res)
def test_3(self):
res = has_path_sum(self.root, 11)
self.assertFalse(res)
def test_4(self):
res = has_path_sum(self.root, 17)
self.assertTrue(res)
考え方:
この問題の解決にも再帰処理を利用します。あるパスを構成するノードの合計は以下のような再帰計算によって求めることになります:
path を構成するノードの合計値 = 現在のノードの値 + それ以下の子ノードの合計値
またこの再帰処理の base case は leaf node (パスの末端に位置するノード) に到達した場合です。
こうした再帰操作を行うためのヘルパー関数として has_sum(root, sum, cur) を定義します。この関数では has_path_sum() が受け取る引数に加えて、ルートノードから現在の階層までのノードの合計値をセットしておく cur 引数も受け取るようにします。この cur の値に今回の再帰処理の対象となるノードの値を加えた時点で、合計値がターゲットである sum と等しいかを比較し、等しく、かつ、このノードが leaf node (つまり left と right の子ノードがともに None) であれば True を返します。
しかしいずれかの条件が満たされていない場合は leaf node に達するまで同じ処理を繰り返すことになります:
プログラム実装例：
from typing import Optional
def has_path_sum(root: Optional[TreeNode], sum: int) -> bool:
def has_sum(root: Optional[TreeNode], sum: int, cur: int) -> bool:
if root is None:
return False
rv = 0 if root.val is None else root.val
cur += rv
if cur == sum and root.left is None and root.right is None:
return True
return has_sum(root.left, sum, cur) or has_sum(root.right, sum, cur)
return has_sum(root, sum, 0)
def has_path_sum(root: Optional[TreeNode], sum: int) -> bool:
def has_sum(root: Optional[TreeNode], sum: int, cur: int) -> bool:
if root is None:
return False
rv = 0 if root.val is None else root.val
cur += rv
if cur == sum and root.left is None and root.right is None:
return True
return has_sum(root.left, sum, cur) or has_sum(root.right, sum, cur)
return has_sum(root, sum, 0)
Complexity Analysis
(アルゴリズム解析)
Time complexity (実行計算時間):
渡されたバイナリツリーを１度だけ走査していますから O(n) です。
Space complexity (実行メモリ要求量):
再帰呼び出しの回数は渡されたバイナリツリーの「高さ (h)」に依存します。またノード数が n のバイナリツリーの最大高さは n ですから O(n) です。