現在の投稿数 177
【 Effective Python, 2nd Edition + coding challenge 】プログラム開発のどの段階で並列処理 ( concurrency ) が必要になるのだろう? そのときどのようにリファクタリング ( refactoring ) していけばいいのだろう? を考えてみるシリーズ ( のはず ) 第1回 投稿一覧へ戻る
Published 2020年8月25日10:18 by mootaro23
SUPPORT UKRAINE
- Your indifference to the act of cruelty can thrive rogue nations like Russia -
プログラムが大きくなってくれば、必然的に、その複雑さも増していきます。
コードの明快さ、テストのし易さ、効率性を維持しながらプログラムを大きくしていくのは、プログラム開発における最も難しい課題のひとつであることは疑う余地がありません。
またプログラムの拡大に伴う変更の中でも、シングルスレッドプログラムのマルチスレッドプログラムへの移行はもっとも困難を伴うもののひとつでしょう。
今後数回は、この問題にどう対処していったらよいのか、ということを取り上げていければ、と考えています。
ということで、このシリーズでは、Conway's Game of Life の実装例で考えていきたいと思っていますので、
今回はこのゲームの coding challenge にしたいと思います。
Conway's Game of Life のルールはいたってシンプルです。
まず、任意の大きさの 2 次元グリッド ( Python では 2 次元のリストで表現します ) を用意します。
グリッド ( grid ) を構成する全てのセル ( cell ) は、生きている ( live ) か死んでいる ( dead ) 状態のどちらかをとります。
プログラムはある 1 単位時間 ( 1 ティック, 1 tick ) で 1 ステップずつ進行します。
あるセルの次のステップにおける状態は、そのセルを取り囲む 8 つのセルの現在のステップにおける状態によって決定します。
もし現ステップで生存しているセルの場合、取り囲む 8 つのセルのうち 2 個もしくは 3 個のセルが生存していれば次のステップも生き続けます。
もし現ステップで死滅している場合、取り囲む 8 つのセルのうちピッタリ 3 個のセルが生存していれば復活 (誕生、生存) します。
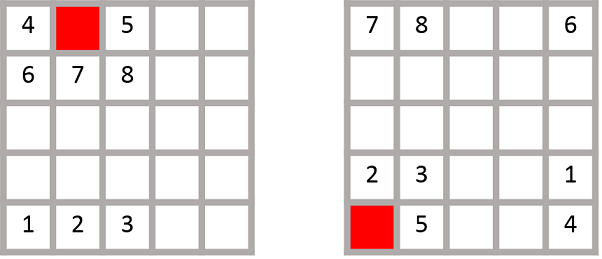
また Conway's Game of Life において、グリッドの上と下、右と左はつながっているものと考えるため、あるセルがグリッドの端にある場合でも、取り囲むセルは常に 8 個存在します。
例えば、5 行 9 列のグリッドにおいて、最初の生存セルが (0, 3), (1, 4), (2, 2), (2, 3), (2, 4) である場合の遷移は次のような表示になります。
このパターンは、左上から右下に向けて斜めに移動しながら「生き延びていく」ものです。
コードの明快さ、テストのし易さ、効率性を維持しながらプログラムを大きくしていくのは、プログラム開発における最も難しい課題のひとつであることは疑う余地がありません。
またプログラムの拡大に伴う変更の中でも、シングルスレッドプログラムのマルチスレッドプログラムへの移行はもっとも困難を伴うもののひとつでしょう。
今後数回は、この問題にどう対処していったらよいのか、ということを取り上げていければ、と考えています。
ということで、このシリーズでは、Conway's Game of Life の実装例で考えていきたいと思っていますので、
今回はこのゲームの coding challenge にしたいと思います。
Conway's Game of Life のルールはいたってシンプルです。
まず、任意の大きさの 2 次元グリッド ( Python では 2 次元のリストで表現します ) を用意します。
グリッド ( grid ) を構成する全てのセル ( cell ) は、生きている ( live ) か死んでいる ( dead ) 状態のどちらかをとります。
LIVE = '■' # 生存セル
DEAD = '□' # 死滅セル
DEAD = '□' # 死滅セル
プログラムはある 1 単位時間 ( 1 ティック, 1 tick ) で 1 ステップずつ進行します。
あるセルの次のステップにおける状態は、そのセルを取り囲む 8 つのセルの現在のステップにおける状態によって決定します。
もし現ステップで生存しているセルの場合、取り囲む 8 つのセルのうち 2 個もしくは 3 個のセルが生存していれば次のステップも生き続けます。
もし現ステップで死滅している場合、取り囲む 8 つのセルのうちピッタリ 3 個のセルが生存していれば復活 (誕生、生存) します。
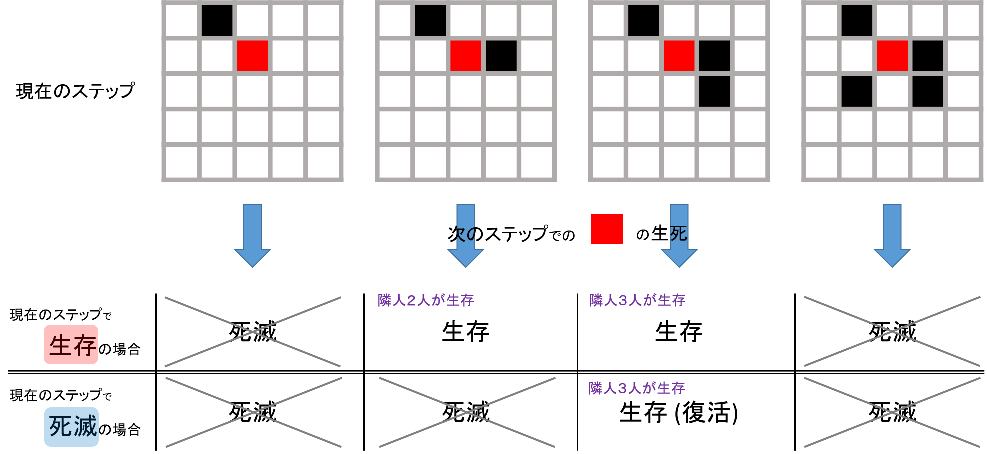
また Conway's Game of Life において、グリッドの上と下、右と左はつながっているものと考えるため、あるセルがグリッドの端にある場合でも、取り囲むセルは常に 8 個存在します。
例えば、5 行 9 列のグリッドにおいて、最初の生存セルが (0, 3), (1, 4), (2, 2), (2, 3), (2, 4) である場合の遷移は次のような表示になります。
□□□■□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□□□□□□
□□□□■□□□□ □□■□■□□□□ □□□□■□□□□ □□□■□□□□□ □□□□■□□□□ □□□□□□□□□
□□■■■□□□□ → □□□■■□□□□ → □□■□■□□□□ → □□□□■■□□□ → □□□□□■□□□ → □□□■□■□□□
□□□□□□□□□ □□□■□□□□□ □□□■■□□□□ □□□■■□□□□ □□□■■■□□□ □□□□■■□□□
□□□□□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□■□□□□
□□□□□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□□■□□□ □□□□□■■□□ □□□□□■■□□
□□□□□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□□□□□□
□□□□□■□□□ → □□□□■□□□□ → □□□□□■□□□ → □□□□□□□□□ → □□□□□□□□□ → □□□□□□□□□
□□□■□■□□□ □□□□□■■□□ □□□□□□■□□ □□□□■□■□□ □□□□□□■□□ □□□□□■□□□
□□□□■■□□□ □□□□■■□□□ □□□□■■■□□ □□□□□■■□□ □□□□■□■□□ □□□□□□■■□
□□□□■□□□□ □□■□■□□□□ □□□□■□□□□ □□□■□□□□□ □□□□■□□□□ □□□□□□□□□
□□■■■□□□□ → □□□■■□□□□ → □□■□■□□□□ → □□□□■■□□□ → □□□□□■□□□ → □□□■□■□□□
□□□□□□□□□ □□□■□□□□□ □□□■■□□□□ □□□■■□□□□ □□□■■■□□□ □□□□■■□□□
□□□□□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□■□□□□
□□□□□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□□■□□□ □□□□□■■□□ □□□□□■■□□
□□□□□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□□□□□□ □□□□□□□□□
□□□□□■□□□ → □□□□■□□□□ → □□□□□■□□□ → □□□□□□□□□ → □□□□□□□□□ → □□□□□□□□□
□□□■□■□□□ □□□□□■■□□ □□□□□□■□□ □□□□■□■□□ □□□□□□■□□ □□□□□■□□□
□□□□■■□□□ □□□□■■□□□ □□□□■■■□□ □□□□□■■□□ □□□□■□■□□ □□□□□□■■□
このパターンは、左上から右下に向けて斜めに移動しながら「生き延びていく」ものです。
では実装してみてください。( 制限時間: 150 分)
ヒント ( になるかな? ):
私は、まず、グリッドを象徴するクラスを用意しました。
このクラスを元に、以下のオブジェクトを作成し表示した結果が、上の出力例の左上のグリッドになります。
このほか、いくつかのヘルパー関数を用意し、最終的にそれらを組み合わせることでシミュレーションを達成しています。
実装例は、次回の記事で掲載します。
では、実装、楽しんでください!
ヒント ( になるかな? ):
私は、まず、グリッドを象徴するクラスを用意しました。
class Grid:
"""
グリッドを象徴する
:param rows: 行数
:param columns: 列数
"""
def __init__(self, rows, columns):
self.rows = rows
self.columns = columns
# 与えられた行数、列数をもつ 2 次元リストを作成する。全ての要素のデフォルト値は DEAD
self.mat = [[DEAD] * self.columns for _ in range(self.rows)]
def get(self, row, column):
"""
対象セルの値 ( 状態: LIVE or DEAD ) を返す
"""
return self.mat[row % self.rows][column % self.columns]
def set(self, row, column, state):
"""
対象セルに値 ( 状態: LIVE or DEAD ) をセットする
"""
self.mat[row % self.rows][column % self.columns] = state
def __str__(self):
"""
このグリッドを象徴する文字列を返す
この文字列は '□□□\n■□□\n□□■\n■■□\n' のように、各列の末尾に '\n' が付加されたもの
"""
result = ''
for row in range(self.rows):
result += ''.join([self.mat[row][column] for column in range(self.columns)]) + '\n'
return result
"""
グリッドを象徴する
:param rows: 行数
:param columns: 列数
"""
def __init__(self, rows, columns):
self.rows = rows
self.columns = columns
# 与えられた行数、列数をもつ 2 次元リストを作成する。全ての要素のデフォルト値は DEAD
self.mat = [[DEAD] * self.columns for _ in range(self.rows)]
def get(self, row, column):
"""
対象セルの値 ( 状態: LIVE or DEAD ) を返す
"""
return self.mat[row % self.rows][column % self.columns]
def set(self, row, column, state):
"""
対象セルに値 ( 状態: LIVE or DEAD ) をセットする
"""
self.mat[row % self.rows][column % self.columns] = state
def __str__(self):
"""
このグリッドを象徴する文字列を返す
この文字列は '□□□\n■□□\n□□■\n■■□\n' のように、各列の末尾に '\n' が付加されたもの
"""
result = ''
for row in range(self.rows):
result += ''.join([self.mat[row][column] for column in range(self.columns)]) + '\n'
return result
このクラスを元に、以下のオブジェクトを作成し表示した結果が、上の出力例の左上のグリッドになります。
grid = Grid(5, 9)
grid.set(0, 3, LIVE)
grid.set(1, 4, LIVE)
grid.set(2, 2, LIVE)
grid.set(2, 3, LIVE)
grid.set(2, 4, LIVE)
print(grid)
# □□□■□□□□□
# □□□□■□□□□
# □□■■■□□□□
# □□□□□□□□□
# □□□□□□□□□
grid.set(0, 3, LIVE)
grid.set(1, 4, LIVE)
grid.set(2, 2, LIVE)
grid.set(2, 3, LIVE)
grid.set(2, 4, LIVE)
print(grid)
# □□□■□□□□□
# □□□□■□□□□
# □□■■■□□□□
# □□□□□□□□□
# □□□□□□□□□
このほか、いくつかのヘルパー関数を用意し、最終的にそれらを組み合わせることでシミュレーションを達成しています。
実装例は、次回の記事で掲載します。
では、実装、楽しんでください!
この記事に興味のある方は次の記事にも関心を持っているようです...
- People who read this article may also be interested in following articles ... -

