Python Coding Challenge - What are all the subsets of a given set of integers?
(Python コーディングチャレンジ [重複のない数値セットにおける全ての組み合わせを求めよう!]編)
(Python コーディングチャレンジ [重複のない数値セットにおける全ての組み合わせを求めよう!]編)
「重複のない数の集まり (セット/集合) を対象にそれらのすべての組み合わせ (重複なし) を求める」という問題は実はかなり複雑な問題です。空のセット [] を土台に集合の各要素を順々に追加していく方法、要素数 n に対応するビット数からなる2進表現を利用する方法、をそれぞれ考えてみましょう。
問題:
重複のない int 値で構成される数値セット nums が与えられます。この時、これらの要素から得られる全ての組み合わせを取得してください。このような組み合わせ集合のことを power set (冪集合 [べきしゅうごう]) と呼びます。
取得する組み合わせには重複があってはいけません。
例:
与えられる数値セット: [1, 2, 3]
出力 (出力される要素の順番、出力フォーマットは問いません):
[
[],
[1],
[2],
[3],
[1, 2],
[1, 3],
[2, 3],
[1, 2, 3]
]
出力 (出力される要素の順番、出力フォーマットは問いません):
[
[],
[1],
[2],
[3],
[1, 2],
[1, 3],
[2, 3],
[1, 2, 3]
]
また関数定義は以下のような形です (同じである必要はありません):
def subsets(self, nums: list[int]) -> list[list[int]]:
...
...
考え方の基本:
重複がない n 個の要素セットにおける重複しない組み合わせの総数は 2ⁿ 個です。問題例で説明すれば、要素 1 を「含む」「含まない」の2通りに対し、それぞれ要素 2 を「含む」「含まない」が考えられるため 2*2 = 2² = 4 通り、そのそれぞれに対して要素 3 を「含む」「含まない」が考えられるため 2*2*2 = 2³ = 8 通り、となるためです。
アプローチ1: 順々に加えていく方法
実装アプローチの1つは、考え方の基本をそのままコードで実現する、というものです。要素 1 を含まない空サブセット [] をスタート地点として、要素 1 を含む場合を考える場合は現在あるすべてのサブセットに 1 を加えたもの、すなわちこの段階ではサブセットは [] だけですから 1 を加えた [1] とそれまでのサブセット [] を合わせた [[], [1]] がここまでの組み合わせとなります。
続いて要素 2 を加える場合、現在あるサブセット [[], [1]] の全ての要素に対して 2 を付け加えたもの [2], [1, 2] をそれまでのサブセットに加えて [[], [1], [2], [1, 2]] となります。この操作を要素数分繰り返していきます。
この操作を行うために for 文のネストループを実装します。外側は与えられる集合セット nums をループして要素 num を取り出し、内側は出力するサブセットを要素とするリスト output をループして要素 curr を取り出します。
そして、curr に num を要素として加えた新しいサブセットを new_output に一時的に保存しておき、すべての output 要素に num を付け加え終えた段階で new_output に保存しておいた num を加えた新たなサブセット群を output に追加して次の num の処理へとループします。
ではもう一度処理を順々に追いかけてみましょう:
nums = [1, 2, 3]
output = [[]]
外側のループ: nums の1番目の要素 num (== 1) を取り出す
new_output = []
内側のループ: output の1番目の要素 [] を取り出し num を追加し (== [1]) new_output に追加する (new_output == [[1]])
output の要素は1つだけのため内側のループを抜けてくるので、output に new_output の要素を追加する (output == [[], [1]])
外側のループ: nums の2番目の要素 num (== 2) を取り出し new_output を [] に初期化する
内側のループ: output の1番目の要素 [] を取り出し num を追加し (== [2]) new_output に追加する (new_output == [[2]])
内側のループ: output の2番目の要素 [1] を取り出し num を追加し (== [1, 2]) new_output に追加する (new_output == [[2], [1, 2]])
内側のループを抜けてくるので、output に new_output の要素を追加する (output == [[], [1], [2], [1, 2]])
外側のループ: nums の3番目の要素 num (== 3) を取り出し new_output を [] に初期化する
内側のループ: output のそれぞれの要素 [], [1], [2], [1, 2] を取り出しつつそれぞれに num を追加し new_output に保存する (new_output == [[3], [1, 3], [2, 3], [1, 2, 3]])
内側のループを抜けてきたら output に new_output の要素を追加する (output == [[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]])
「アプローチ1: 順々に加えていく方法」の実装例:
def subsets(self, nums: list[int]) -> list[list[int]]:
output: list[list[int]] = [[]]
for num in nums:
new_output = []
for curr in output:
new_output += [curr + [num]]
output += new_output
return output
if __name__ == '__main__':
res = subsets([1, 2, 3])
print(res)
output: list[list[int]] = [[]]
for num in nums:
new_output = []
for curr in output:
new_output += [curr + [num]]
output += new_output
return output
if __name__ == '__main__':
res = subsets([1, 2, 3])
print(res)
# 出力: [[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]
Complexity Analysis
(アルゴリズム解析 - 実行時間解析)
外側のループは与えられた集合セットの要素数分ループしますから n 回実行されます。内側のループは作成するサブセット数分実行します (外側のループが繰り返される毎に倍になっていきます) から O(2ⁿ) となります。よってプログラム全体の時間計算量 (time complexity) は O(n2ⁿ) となります。
アプローチ2: ビット表現を利用する方法
「考え方の基本」をビット表現に置き換えて考える方法です。
「考え方の基本」で説明したように、与えられた集合セットの要素 1 を「含む (1)」「含まない (0)」それぞれのパターンにおいて要素 2 を「含む (1)」「含まない (0)」パターンが存在し、これが要素数分繰り返されていきます。
ですから全てのサブセット (組み合わせ) それぞれにおいて、集合セットの要素数 n 分のビット数からなるユニークなビットの組み合わせが 2ⁿ 個存在する、ということになります:
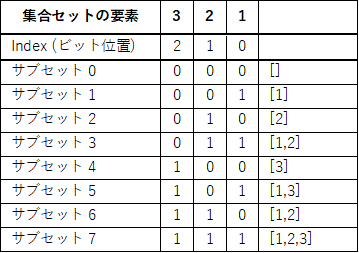
Binary representation of subsets
- Shyamkant Limaye (2021). Python Quick Interview Guide. BPB Publications -
この実装方法でもループのネストを利用します。外側のループ i は作成するサブセットの総数分 (2ⁿ) ループし、内側のループ j は要素数分 (n) ループします。
内側のループでは最下位のビットが立っている (1) かどうかを調べ(2 で割った時に余りがあれば最下位ビットは 1 ということです)、もし最下位ビットが立っていればその要素 (nums[j]) を一時的なサブセットリストに追加します。同様に次のビットを調べますが、次のビットを最下位ビットに「移動」するために 2 で割ることになります。
この操作を全ての要素数分繰り返し、出来上がった一時的サブセットの内容を「リストとして」出力する output リストに追加します。
この操作では、記載した画像を見てもらえれば分かるようにインデックス 0 がビット番号 1 に対応しますから、ビットの処理は LSB (Least Significant Bit: 最下位ビット) 優先で行うことになります:
「アプローチ2: ビット表現を利用する方法」の実装例:
def subsets(self, nums: list[int]) -> list[list[int]]:
n = len(nums)
output: list[list[int]] = []
for i in range(2 ** n):
temp = i
temparr = []
for j in range(n):
if temp % 2:
temparr.append(nums[j])
temp = temp // 2
output += [temparr]
return output
if __name__ == '__main__':
res = subsets([1, 2, 3])
print(res)
n = len(nums)
output: list[list[int]] = []
for i in range(2 ** n):
temp = i
temparr = []
for j in range(n):
if temp % 2:
temparr.append(nums[j])
temp = temp // 2
output += [temparr]
return output
if __name__ == '__main__':
res = subsets([1, 2, 3])
print(res)
# 出力: [[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]
Complexity Analysis
(アルゴリズム解析 - 実行時間解析)
外側のループは作成するサブセットの総数分ループしますから 2ⁿ 回実行されます。内側のループは与えられた集合セットの要素数分ループしますから n 回実行されます。よってプログラム全体の時間計算量 (time complexity) は O(n2ⁿ) となります。
アプローチ2の変化型:
アプローチ2 において Python の関数をもう少しうまく利用することを考えてみましょう。
Python には int 値を受け取って対応する 2 進数の文字列を返してくれる bin() が用意されています:
bin(1) -> '0b1'
bin(3) -> '0b11'
bin(6) -> '0b110'
bin(3) -> '0b11'
bin(6) -> '0b110'
しかしこの bin() を今回のプログラムで利用するには問題点が2つあります。1つは返される文字列の先頭に '0b' がついていること、もう1つは与えられる2進数の桁数が集合セットの要素数 n と必ずしも一致しないこと、です。
1つ目の「'0b' が先頭にくっついてくる」問題は「スライス」処理で対応できます:
bin(1)[2:] -> '1'
bin(3)[2:] -> '11'
bin(6)[2:] -> '110'
bin(3)[2:] -> '11'
bin(6)[2:] -> '110'
2つ目の「桁数が合わない」問題は string クラスの zfill() を利用することで対応可能です:
bin(1)[2:].zfill(3) -> '001'
bin(3)[2:].zfill(3) -> '011'
bin(6)[2:].zfill(3) -> '110'
bin(3)[2:].zfill(3) -> '011'
bin(6)[2:].zfill(3) -> '110'
さてこれらを利用すると最初のアプローチ2の実装は次のようになるでしょうか:
「アプローチ2変化型: もっと pythonic な方法」の実装例:
def subsets(self, nums: list[int]) -> list[list[int]]:
n = len(nums)
output: list[list[int]] = []
for i in range(2 ** n):
temparr = []
bits = bin(i)[2:].zfill(n)
output += [[nums[j] for j in range(n) if bits[j] == '1']]
return output
if __name__ == '__main__':
res = subsets([1, 2, 3])
print(res)
n = len(nums)
output: list[list[int]] = []
for i in range(2 ** n):
temparr = []
bits = bin(i)[2:].zfill(n)
output += [[nums[j] for j in range(n) if bits[j] == '1']]
return output
if __name__ == '__main__':
res = subsets([1, 2, 3])
print(res)
# 出力: [[], [3], [2], [2, 3], [1], [1, 3], [1, 2], [1, 2, 3]]
出力結果が変わっていることに気付きましたか? これはこの実装方法では最上位ビット (MSB: Most Significant Bit) から処理を行なっているためです。また実行時間解析に変化はありません。
アプローチ3: もっと Pythonic に楽をする方法
Python の itertools ライブラリには combinations() が含まれています。combinations(iterable, r) は、iterable の要素から長さ r の重複のない組み合わせを tuple として提供するイテレータを返します:
for i in combinations([1, 2, 3], 2):
print(i)
print(i)
# 出力:
# (1, 2)
# (1, 3)
# (2, 3)
これを利用すると次のように記述できます:
Python の itertools ライブラリ combinations 関数を利用した実装例:
def subsets(self, nums: list[int]) -> list[list[int]]:
result = [list(i) for c in range(len(nums) + 1) for i in combinations(nums, c)]
return result
if __name__ == '__main__':
res = subsets([1, 2, 3])
print(res)
result = [list(i) for c in range(len(nums) + 1) for i in combinations(nums, c)]
return result
if __name__ == '__main__':
res = subsets([1, 2, 3])
print(res)
# 出力: [[], [1], [2], [3], [1, 2], [1, 3], [2, 3], [1, 2, 3]]

