Python Coding Challenge - How will you detect a redundant road connection?
(Python コーディングチャレンジ [無向グラフにおいて閉路 (cycle) を形成している辺 (edge) を見つけて connected-acyclic グラフ == ツリーにしよう!] 編)
(Python コーディングチャレンジ [無向グラフにおいて閉路 (cycle) を形成している辺 (edge) を見つけて connected-acyclic グラフ == ツリーにしよう!] 編)
N 個の都市からなる国を想像してください。この国では現在各都市を結ぶ高速道路網を整備しようとしています。都市間をどのように結ぶか、に関する複数の案が担当省庁に提案されましたが、予算の都合上、接続されていない都市がないことを条件に最小限の高速道路の建設のみを認可することにしました。しかし選考過程にミスが生じ冗長なルートが1つ認可されてしまいました。つまりこのルートを削除したとしても各都市は全て接続されたまま、ということです。このルート (接続: edge) を見つけられますか?
この問題では disjoint-set data structure (素集合データ構造: union-find algorithm) の知識を学習します。
問題:
1 から N までの番号がふられた頂点 (vertices) からなる無向 graph を考えます (高速道路は一方通行ではありませんから)。このグラフは edges のリストで表現されています。例えば [[1, 2], [2, 3]] であれば、都市 1 と都市 2 を結ぶ edge [1, 2]、都市 2 と都市 3 を結ぶ edge [2, 3]、という具合です。
与えられる edges リストの要素にはツリーデータ構造を「壊す」edge が含まれている場合があります。つまり、その edge が存在するためにグラフに循環 (cycle) が生じている場合がある、というわけです。この edge を除去することができれば循環がなくなり「グラフをツリーにする」ことができます。この edge を見つけるためのプログラムを記述してください。
しかし「循環をなくす」ための edge が一意に決まるとは限りません。結果的にその edge を削除することで「循環」がなくなりデータ構造がツリーになれば OK とします。
また、必ずしも「循環」が生じているとも限りません。もし与えられたデータに「循環」が含まれていなければ None を返してください。
例 1:
与えられるリスト: [[1, 2], [1, 3], [2, 3]]
# 出力: [2, 3]
例 1 の解説:
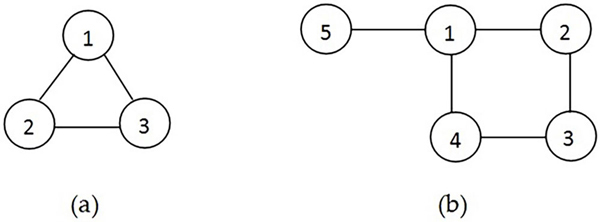
与えられたデータが表現しているグラフは下図の (a) です。これらの edges のうちどれか1つを取り除けば循環が消滅し「接続していて循環がない」グラフ、つまり、ツリーになります。よって答えは [2, 3] ですが、[1, 2] もしくは [1, 3] であっても正解です。
例 2:
与えられるリスト: [[1, 2], [2, 3], [3, 4], [1, 4], [1, 5]]
# 出力: [1, 4]
例 2 の解説:
与えられたデータが表現しているグラフは下図の (b) です。この graph では [1-2-3-4-1] で循環が形成されています。ですから、この循環を形成しているいずれか1本の edge を取り除けば循環が解消されます。よって [1, 2], [1, 4], [2, 3], [3, 4] のいずれかが正解になります。
また関数定義は以下のような形です (同じである必要はありません):
def find_redundant_connection(edges: list[list[int]]) -> list[int]:
...
...
作成したプログラムは以下のテストをパスする必要があります:
import unittest
class TestFindRedundantConnection(unittest.TestCase):
def test_1(self):
edges = [[1,2], [1,3], [2,3]]
res = find_redundant_connection(edges)
self.assertEqual(res, [2, 3])
def test_2(self):
edges = [[1,2], [1,3]]
res = find_redundant_connection(edges)
self.assertIsNone(res)
def test_3(self):
edges =[[1,2], [2,3], [3,4], [1,4], [1,5]]
res = find_redundant_connection(edges)
self.assertEqual(res, [1, 4])
def test_4(self):
edges = [[1, 2], [2, 3], [3, 4], [3, 5], [2, 6], [1, 7], [1, 8], [8, 9], [9, 10], [9, 11], [8, 12], [11, 12]]
res = find_redundant_connection(edges)
self.assertEqual(res, [11, 12])
if __name__ == '__main__':
unittest.main()
class TestFindRedundantConnection(unittest.TestCase):
def test_1(self):
edges = [[1,2], [1,3], [2,3]]
res = find_redundant_connection(edges)
self.assertEqual(res, [2, 3])
def test_2(self):
edges = [[1,2], [1,3]]
res = find_redundant_connection(edges)
self.assertIsNone(res)
def test_3(self):
edges =[[1,2], [2,3], [3,4], [1,4], [1,5]]
res = find_redundant_connection(edges)
self.assertEqual(res, [1, 4])
def test_4(self):
edges = [[1, 2], [2, 3], [3, 4], [3, 5], [2, 6], [1, 7], [1, 8], [8, 9], [9, 10], [9, 11], [8, 12], [11, 12]]
res = find_redundant_connection(edges)
self.assertEqual(res, [11, 12])
if __name__ == '__main__':
unittest.main()
考え方:
「冗長な edge が存在しているか」だけを判断するのは非常に簡単です。この graph theory シリーズの初回「グラフ理論の基礎」 でも復習した通り、connected-acyclicグラフ、つまりツリーにおいては Vertices = Edges + 1 の関係が成り立ちます。Edge から考えれば E = V - 1 です。ですから E > V - 1 であればそのグラフには冗長な edge が存在する、つまり「閉路」が存在する、ということです。
しかし「冗長な edge を特定する」ためにはもう少し労力を必要とします。この問題の最もシンプルな解決方法は、the union of disjoint sets methodology (素集合の和を利用する方法) です。与えられた edges の情報からまず最初に「重複のないノードの集合」を作成し、続けて edges の情報を1つ1つ読み込みながら graph を作成していきます。この時、「与えられた edges」が「接続している循環のない graph == tree」を表現しているものであれば「重複のないノードの集合」から作成される「素集合の森」にはただ1つの素集合しか存在しません。この場合プログラムからは None が返ります。
しかし、もし作成している「素集合の森」の中に同じルートノードをもつ素集合が2つ以上できた場合は「与えられた edges」は「循環」箇所を含む graph を表現している、ということであり、それができた時点に処理していた edge が「循環を生み出している冗長な edge」ですからプログラムからはこの edge を返します。
スタート地点はまったく edge を含まない N 個のノードの集合です。そしてこれらのノードが「接続しているノード」の集合、すなわち「素集合の森」に属している、と仮定します。それぞれの素集合は「1つのルートノード」によって識別されます。初期段階では edge は1つも存在していません。つまり、この「素集合の森」の中にはノードの数 N 個と同じ数だけの素集合が存在し、それぞれの素集合のルートノードはそれぞれのノード自分自身、ということになっています。
プログラムではまず「接続しているノード」集合のルートノードを要素とする配列 p を定義します。初期段階では1つの edge も存在しない、つまり「接続しているノード」集合はルートノードだけから成り立っている状態です。つまり、それぞれのノードのルートノードは自分自身、ですね。ですから、あるノードがルートノードであるかを確認するためのテストでは p[i] == i が成り立つ必要があります。もしノードが N 個であれば p の初期値は [0, 1, 2, 3, 4, ..., N] です (要素として 0 を含んでいるのはノードの data/entry が 1 から始まっている、として処理しているためです。配列 p の要素であるルートノードと、配列 p のインデックス番号が表すノード自身を一致させるために p を 0 から始める必要があります。こうすることで p[i] == i が成り立ちます)。
続いて edge(x, y) を graph に追加します。つまり x と y を接続するわけです。この操作は union と呼ばれていて、2つのルートノードのどちらかをもう1つのルートノードに結合する作業です。そして、どちらか一方のノードをもう1つのノードの「親 (parent)」と見なします。今回の実装例では y を x の親として扱います。ですから edge(x, y) から y をルートノードとする素集合を作成したことになります。
頭を整理しよう (get organized) Part.1:
ここで扱っている p 配列の「要素」はあくまでも「ルートノード」を表現しています。そして「そのルートノード」に属しているノードは p 配列の「インデックス番号」が表現しているノードです。例えば p の初期値が [0, 1, 2, 3] 、edge(1, 2) において x = 1, y = 2 です。ここで x を y に union する (p[x] = p[y]) と p[0, 2, 2, 3] になりますね。このとき p[1] が表現していることは、「2 をルートノードとする集合にノード 1 が含まれている」ということです。「あれっ、ノード 1 が消えちゃったよー (泣)」と途方に暮れてはダメですよ!
この操作を続けていくと、新たな処理対象となる edge(x, y) のノード x とノード y は「ルートノード」か「いずれかのルートの子ノード」になります。ここで必要なのは x と y が同じルートノードを親としていないか、を確認する作業です。その処理を行なうために find() を定義します。この関数は再帰関数として実装し、自分が属している集合のルートノードが見つかるまで再帰処理を行ないます。この再帰処理の base case (再帰操作を終了する条件) は「自分の親ノードが自分自身」になった時です。そしてこの時点でルートノードを返します。
頭を整理しよう (get organized) Part.2:
「頭を整理しよう Part.1」の続きとして考えます。p[0, 2, 2, 3] であるときに edge(1, 3) が与えられたとします。x = 1 ですね。ここでノード 1 が属している素集合のルートノードを求めるために find(x) を呼び出します。自分自身は勿論 x == 1 == 「p のインデックス番号 (i としましょう)」 です。この時 x のルートノードは p[x] == p[i] == p[1] == 2 です。x != 2 ですね。ベースケースではありませんから find(1) から返された値 (== 2) を引数として再び自分自身を呼び出します; つまり find(p[x]) == find(2) です。今回の自分自身は x == 2 == 「p のインデックス番号」です。この時 x のルートノードは p[x] == p[i] == p[2] == 2 です。x == 2 ですね。ベースケースにマッチしますから find(2) は見つかったルートノード p[x] == p[2] == 2 を返します。結果として、ノード 1 のルートノードは 2 である、ということです。
そしてもう1つの関数 union() で edge で接続されているノード x とノード y のそれぞれのルートノードが同じかどうかをチェックします。もし同じであれば、素集合の森の中に同じルートノードで識別される集合が複数存在する、ということになり、今回処理した edge が「循環を構成する冗長な edge」ということになりますから答えとしてこの edge を返して処理を終了します。しかしルートノードが異なる場合はこれら2つの素集合を1つにまとめる union 操作を行います。先述しましたが、今回のプログラムでは y を x の親とします。
find()、union() とも find_redundant_connection() の内部関数として定義します。find_redundant_connection() がやっていることは、与えられた edges 配列から配列 p を初期化することと、edges 配列をループしながら union() を呼び出すことだけです。
ここでちょっと躓くとしたら p の初期化作業でしょう。もし与えられた edges が connected-acyclic graph、 つまり tree を表現しているのであれば、そのノード数 V は最大で V = E + 1 です。しかしノードの番号を 1 から始めていますから +1 をしないとインデックス番号とノード番号との整合が取れません。
よって 配列 p の要素数 V は (E + 1 + 1) == (E + 2) となります。
プログラム実装例:
from typing import Optional
def find_redundant_connection(edges: list[list[int]]) -> Optional[list[int]]:
p: list[int] = [x for x in range(len(edges)+2)]
if p[x] != x:
p[x] = find(p[x])
return p[x]
if find(x) == find(y):
return True
p[find(x)] = find(y)
return None # 省略可能: 型チェッカー Mypy でエラーを出さないため記述
for x, y in edges:
if union(x,y):
return [x, y]
return None # 省略可能: 型チェッカー Mypy でエラーを出さないため記述
def find_redundant_connection(edges: list[list[int]]) -> Optional[list[int]]:
p: list[int] = [x for x in range(len(edges)+2)]
# ルートノードの探索
def find(x) -> int:if p[x] != x:
p[x] = find(p[x])
return p[x]
# 2つの素集合の結合
# 2つのノードのルートノードが一致 -> 循環
def union(x, y) -> Optional[bool]:if find(x) == find(y):
return True
p[find(x)] = find(y)
return None # 省略可能: 型チェッカー Mypy でエラーを出さないため記述
for x, y in edges:
if union(x,y):
return [x, y]
return None # 省略可能: 型チェッカー Mypy でエラーを出さないため記述
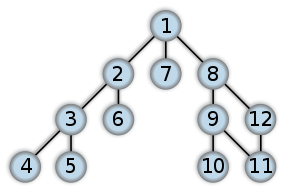
ここでユニットテスト 4 の edges が表現している graph の図を載せておきます。プログラムの実行結果では「冗長な edge」は [11, 12] ですが、循環は [8-9-11-12-8] に存在しています。ですからこの循環を形成しているいずれかの edge が正解になります。
Complexity Analysis
(アルゴリズム解析)
Time complexity (実行計算時間):
頂点 (ノード: vertices) の数は E+1 です。外側のループは E+1 実行されます。find() の再起呼び出しも最大で E+1 実行され、これが union() の中で2回呼び出されています。よってプログラム全体では O((E+1)*2*(E+1)) となりますが、注目するのは係数、定数を除いた最大次数の項だけですから O(E²) です。
Space complexity (実行メモリ要求量):
頂点の数に等しい配列 p を作成しています。よって O(E) です。