RSSフィードを購読
Basics of Graph Theory Part.2 - Representation and Manipulation of Graphs
(グラフ理論の基礎 その２ - グラフの表現と操作)
(グラフ理論の基礎 その２ - グラフの表現と操作)
Graph (グラフ) は非線形データ構造 (nonlinear data structure) です。今回はグラフの表現方法を復習すると同時に、グラフの作成、edges の挿入、出力を行う機能を備えたクラスを定義してみましょう。
Representation
(表現方法)
グラフをコードで表現する方法には次の２つがあります:
Adjacency matrix (隣接行列)
Adjacency list (隣接リスト)
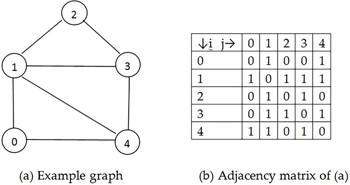
例えば n 個の vertexes (V) を含むグラフ G を考えます。この時 G を表現する隣接行列 A は n x n 行列となります。この隣接行列 A において、A[i][j] = 1 であれば Vi と Vj の vertexes ペアは「接続されている」ということを表します。
無向グラフ (undirected graph) を表す隣接行列は「対称 (symmetric)」です。つまり、Vi から Vj への経路 (path) が存在する場合は Vj から Vi への経路も存在する、ということです。
以下の図は、グラフダイアグラムとそのグラフを隣接行列を利用して表現した例です:
隣接行列を利用した Graph の表現例
- Shyamkant Limaye (2021). Python Quick Interview Guide. BPB Publications -
隣接行列を利用したグラフ表現は「データ操作」の面では非常に便利ですが「メモリ消費」を考えたときには非常にコストの高いものになります。それは、現実に利用するグラフのほとんどはデータが「まばら」、つまり、edges の数が非常に少ないためです。
「まばら」なグラフを扱う有効な手段が「隣接リスト (adjacency list) です。ここで「隣接行列」を「行の配列」であると仮定してみましょう。それぞれの「行」は「頂点 (vertex)」に対応します。そして、他のすべての頂点に対して「接続している (1)」か「接続していない (0)」か、を考える代わりに、「接続している」頂点だけを保存するようにします。この情報をリストとして保存したものが隣接リストです。実装するリストは linked list である必要はありません。Python で一般的に利用している通常の list で何ら支障はありません。
しかし、頂点の情報 (identifiers / ids) が連続する int 値ではない場合も考えられます; 例えば任意の文字列かもしれません。このような場面では list ではなく dictionary を利用して該当グラフを表現する方がお薦めです。この場合、vertex の ID が dictionary のキー (key) となり、接続している頂点の情報を要素とするリストが値 (value) となります。
また dictionary を利用することで各行の検索をより速く実行できるようになる、という利点もあります。しかし通常の dictionary には「望ましくない」特徴がありますね。それは、存在しないキーを検索してしまった場合に例外が投げられ、適切な対処を行っていなければプログラムが終了してしまう、ということです。しかし Python の collections モジュールには defaultdict クラスが用意されています。通常の dictionary を利用する代わりに defaultdict クラスを使用することでこの問題にスマートに対応できます。是非 defaultdict の使い方に習熟しておくようにしましょう！
さて、先述したグラフを隣接リストで表現してみましょう:
0: [1, 4]
1: [0, 2, 3, 4]
2: [1, 3]
3: [1, 2, 4]
4: [0, 1, 3]
1: [0, 2, 3, 4]
2: [1, 3]
3: [1, 2, 4]
4: [0, 1, 3]
Manipulation of graphs
(グラフの操作)
無向グラフ (undirected graph) の機能を象徴する Graph クラスを実装してみましょう。ここでは「隣接リスト」でグラフを表現することにします。実装する機能は「初期化」「edge の追加」「グラフの出力」です。
「初期化」ではグラフの情報をセットする defaultdict(list) オブジェクトを作成します。「edge の追加」機能の定義は insert_edge(self, v1, v2) とします。このメソッドの操作の内容は、v1 と接続している vertex として v2 を追加し、同時に、v2 と接続している vertex として v1 を追加する、というものです。「グラフの出力」機能では全ての情報をプリントアウトします。
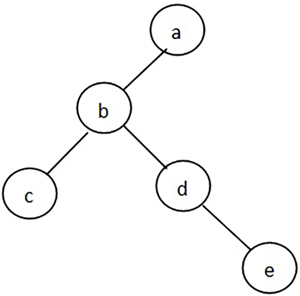
ここでは例として次のようなグラフを作成することにします:
例題で作成するグラフ
- Shyamkant Limaye (2021). Python Quick Interview Guide. BPB Publications -
実装コード例:
from collections import defaultdict
from typing import Any
class Graph:
"""
グラフ (隣接リスト表現)
"""
def __init__(self):
self.graph: defaultdict[Any, list[Any]] = defaultdict(list)
def insert_edge(self, v1, v2):
self.graph[v1].append(v2)
self.graph[v2].append(v1)
def print_graph(self):
for node in self.graph:
print(f'node {node}: {" ".join(self.graph[node])}')
if __name__ == '__main__':
g = Graph()
g.insert_edge('a', 'b')
g.insert_edge('b', 'c')
g.insert_edge('b', 'd')
g.insert_edge('d', 'e')
g.print_graph()
from typing import Any
class Graph:
"""
グラフ (隣接リスト表現)
"""
def __init__(self):
self.graph: defaultdict[Any, list[Any]] = defaultdict(list)
def insert_edge(self, v1, v2):
self.graph[v1].append(v2)
self.graph[v2].append(v1)
def print_graph(self):
for node in self.graph:
print(f'node {node}: {" ".join(self.graph[node])}')
if __name__ == '__main__':
g = Graph()
g.insert_edge('a', 'b')
g.insert_edge('b', 'c')
g.insert_edge('b', 'd')
g.insert_edge('d', 'e')
g.print_graph()
実行結果は次のようになります:
node a: b
node b: a c d
node c: b
node d: b e
node e: d
node b: a c d
node c: b
node d: b e
node e: d