DFS (Depth First Search) Traversal of Graphs and Trees
(「深さ優先探索」によるグラフ及びツリーの探索)
(「深さ優先探索」によるグラフ及びツリーの探索)
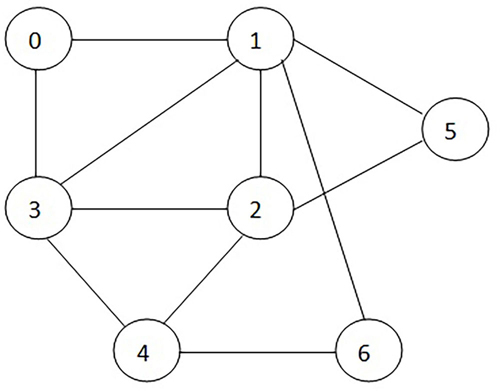
今回から graph および tree における DFS (Depth First Search: 深さ優先探索) を取り上げていきます。シリーズの最初として、DFS を利用したグラフ/ツリーの初期化、edges の追加、出力を行う機能を備えた graph クラスを作成し、次回以降の coding challenge の準備をしましょう。今回は下図の graph を対象に話を進めていきます:
最初は理解がしやすいと思われる「反復操作 (iterative approach)」を学習します。この操作では graph を隣接リスト (adjacency list) の形式で扱います。今回例として取り上げる graph を隣接リストで表現すると次のようになります:
0: [1, 3]
1: [2, 3, 5, 6]
2: [3, 4, 5]
3: [4]
4: [6]
1: [2, 3, 5, 6]
2: [3, 4, 5]
3: [4]
4: [6]
無向グラフを扱う問題では、接続元の vertex の隣接リストに接続先の vertex を加え、接続先の vertex の隣接リストに接続元の vertex を加えることが必要です。しかしここで扱う問題に関してはこうした双方向の入力は必要ではありません。しかしそのやり方の方が馴染みがあるのであればそれはそれで問題はありません。
今回実装するプログラムで使用する変数を以下に列挙します:
g: graph を隣接リスト形式で表現したものです
cur: 現在処理対象となっているノードです
visited: すでに処理を終えたノードのリストです
st: これから処理を行なう必要があるノードを保存しておくためのスタックです
cur: 現在処理対象となっているノードです
visited: すでに処理を終えたノードのリストです
st: これから処理を行なう必要があるノードを保存しておくためのスタックです
DFS algorithm (深さ優先探索アルゴリズム) の基本的な操作の流れは次のようになります:
初期化処理: visited リストを定義します。このリストは同じノードを複数回処理しないために利用します。つづいて st スタックを定義します。最初に処理する任意のノードを1つだけ積んでおきます。これで用意が整いましたから st が空になるまでループ処理を行います。
スタック st の最上段に積まれているノードを pop して変数 cur にセットします。このノードが visited リストに含まれていなければ出力し、visited リストに追加します。
続けて cur に隣接するノードをスキャンします。それぞれのノードにおいて visited リストに含まれていないものはスタック st に追加します。
スタックが空でなければステップ 2 からの操作を繰り返します。このループ操作の終了条件は「スタックが空になった」ときです。
この流れを、例として先ほど挙げた graph を利用して再度確認してみましょう。初期化操作において、スタックにはノード 0 が積まれており visited リストは空の状態です。
スタックの最上段に積まれているノード 0 (例) を取り出し変数 cur にセットします。ノード 0 は visited リストには含まれていませんから出力し visited リストに追加します。続いてノード 0 に隣接するノードをチェックします; 1 と 3 ですね。これらのノードはどちらも visited リストには含まれていませんからスタックに積みます。この時点における visited と st の値は以下のようになっています:
visited = [0]
st = [1, 3]
st = [1, 3]
スタックは空ではありませんからステップ 2 から操作を繰り返します。スタックの最上段に積まれているノード 3 を取り出し変数 cur にセットします。visited には含まれていませんから出力し、visited リストに追加し、隣接するノードをチェックします; 4 です。ノード 4 は visited リストには含まれていませんからスタックに積みます。この時点における visited と st の値は以下のようになっています:
visited = [0, 3]
st = [1, 4]
st = [1, 4]
この操作をスタックが空になるまで続けます。それぞれのステップにおける cur, visited, st 変数の変化を追ってみると次のようになります:
cur visited st
Step 1: 0 [0] [1, 3]
Step 2: 3 [0, 3] [1, 4]
Step 3: 4 [0, 3, 4] [1, 6]
Step 4: 6 [0, 3, 4, 6] [1]
Step 5: 1 [0, 3, 4, 6, 1] [2, 5]
Step 6: 5 [0, 3, 4, 6, 1, 5] [2]
Step 7: 2 [0, 3, 4, 6, 1, 5, 2] []
Step 1: 0 [0] [1, 3]
Step 2: 3 [0, 3] [1, 4]
Step 3: 4 [0, 3, 4] [1, 6]
Step 4: 6 [0, 3, 4, 6] [1]
Step 5: 1 [0, 3, 4, 6, 1] [2, 5]
Step 6: 5 [0, 3, 4, 6, 1, 5] [2]
Step 7: 2 [0, 3, 4, 6, 1, 5, 2] []
このプログラムを実行した際の出力は 0 3 4 6 1 5 2 となります (出力した順番に visited リストに追加していっていますから当然 visited リストの要素と同じ並びです)。プログラムの初期化処理でスタックに積んでおくノード、および、ステップ 3 でスタックに積む隣接ノードの順番は「任意」ですから、DFS におけるノードの探索順番は一意に決まるわけではありません。
この順番を一意に決めたいのであれば、隣接ノードをスタックに積む順番を決めるルールを定めそれに従うようにします。一般的に採用されるルールの1つは、ノードの識別子のアルファベット順にスタックに積む、というものです。これを実現するには隣接リストの要素をソートしておくようにします。
ここまでのプログラムで採用しているアルゴリズムでは、初期化処理の段階でスタックに積んだ「開始ノード」に「接続している」ノードしか出力対象になりません。もし与えられた graph が互いに接続していない集合から成り立っている場合 (disjoint graph)、全てのノードが出力されるわけではありません。こうした状況にも対処するためには、「接続されているノードの集合」を処理するループを抜けてきた時点でまだ処理していないノードが残っていないかを確認し、残っていればそのいずれかのノードを「開始ノード」として同じ処理を繰り返すようにする必要があります。ですから「全てのノードを出力する」プログラムの終了条件は「処理していないノードが残っていない」ことです。
このアルゴリズムを実装したコードが以下になります:
from collections import defaultdict
class Graph:
def __init__(self):
self.graph = defaultdict(list)
self.all_nodes: set[int] = set() # disjoint graph 用 (全てのノードを列挙)
def insert_edge(self, v1: int, v2: int):
"""
edge が1つずつ渡される場合に graph に追加する
"""
self.graph[v1].append(v2)
self.all_nodes.add(v1)
self.all_nodes.add(v2)
def make_graph_from_list(self, ad_list: list[list[int]]):
"""
edges が list の list として渡されたときに graph を作成する
param ad_list: [[1, 2], [1, 3], ...]
"""
for v1, v2 in ad_list:
self.graph[v1].append(v2)
self.all_nodes.add(v1)
self.all_nodes.add(v2)
def depth_first_search(self):
break
visited: set[int] = set()
st: list[int] = [start_node]
while st:
cur = st.pop()
if cur not in visited:
print(cur, end=' ') # 標準出力用
visited.add(cur)
for ad_node in self.graph[cur]:
if ad_node not in visited:
st.append(ad_node)
self.all_nodes -= visited
print() # disjoint graph の場合の標準出力改行用
if __name__ == '__main__':
g = Graph()
g.make_graph_from_list(
[[0, 1], [0, 3], [1, 2], [1, 3], [1, 5], [1, 6], [2, 3], [2, 4], [2, 5], [3, 4], [4, 6]]
)
g.depth_first_search()
g.make_graph_from_list([[1, 2], [1, 3], [2, 4], [2, 5], [6, 7], [7, 8]])
g.depth_first_search()
class Graph:
def __init__(self):
self.graph = defaultdict(list)
self.all_nodes: set[int] = set() # disjoint graph 用 (全てのノードを列挙)
def insert_edge(self, v1: int, v2: int):
"""
edge が1つずつ渡される場合に graph に追加する
"""
self.graph[v1].append(v2)
self.all_nodes.add(v1)
self.all_nodes.add(v2)
def make_graph_from_list(self, ad_list: list[list[int]]):
"""
edges が list の list として渡されたときに graph を作成する
param ad_list: [[1, 2], [1, 3], ...]
"""
for v1, v2 in ad_list:
self.graph[v1].append(v2)
self.all_nodes.add(v1)
self.all_nodes.add(v2)
def depth_first_search(self):
# disjoint graph にも対応するため「全てのノードを処理するまで」処理を続ける
while self.all_nodes: # set に含まれる任意の1つの要素を開始ノードとして参照する
# set 本来の使い方からは少し外れている
for start_node in self.all_nodes:break
visited: set[int] = set()
st: list[int] = [start_node]
while st:
cur = st.pop()
if cur not in visited:
print(cur, end=' ') # 標準出力用
visited.add(cur)
for ad_node in self.graph[cur]:
if ad_node not in visited:
st.append(ad_node)
self.all_nodes -= visited
print() # disjoint graph の場合の標準出力改行用
if __name__ == '__main__':
g = Graph()
g.make_graph_from_list(
[[0, 1], [0, 3], [1, 2], [1, 3], [1, 5], [1, 6], [2, 3], [2, 4], [2, 5], [3, 4], [4, 6]]
)
g.depth_first_search()
# 出力例: 0 3 4 6 1 5 2
# disjoint graph の例
g = Graph()g.make_graph_from_list([[1, 2], [1, 3], [2, 4], [2, 5], [6, 7], [7, 8]])
g.depth_first_search()
# 出力例: 1 3 2 5 4
# 6 7 8
続いて再帰操作による実装を考えてみましょう。
まず再帰関数をラップするインスタンスメソッド depth_first_search() を定義します。このメソッドは graph を構成する全てのノードを処理し終えるまで動作します。visited リストを初期化し、任意の開始ノードを取得し、再帰関数 dfs() を呼び出します。
再帰処理のアルゴリズムは非常に単純です。渡されてきたノードが visited リストに含まれていなければ出力し visited リストに追加します。続けて隣接ノードをチェックし、それを開始ノードとして自分自身を呼び出します。
この再帰アルゴリズムを実装したコード例が次のものになります:
from collections import defaultdict
class ProcGraphRecursively:
def __init__(self):
self.graph = defaultdict(list)
self.all_nodes: set[int] = set() # disjoint graph 用 (全てのノードを列挙)
def insert_edge(self, v1: int, v2: int):
"""
edge が1つずつ渡される場合に graph に追加する
"""
self.graph[v1].append(v2)
self.all_nodes.add(v1)
self.all_nodes.add(v2)
def make_graph_from_list(self, ad_list: list[list[int]]):
"""
edges が list の list として渡されたときに graph を作成する
param ad_list: [[1, 2], [1, 3], ...]
"""
for v1, v2 in ad_list:
self.graph[v1].append(v2)
self.all_nodes.add(v1)
self.all_nodes.add(v2)
def depth_first_search(self):
def dfs(self, node: int):
if node not in self.visited:
print(node, end=' ')
self.visited.add(node)
for ad_node in self.graph[node]:
dfs(self, ad_node)
while self.all_nodes:
self.visited: set[int] = set()
for start_node in self.all_nodes:
break
dfs(self, start_node)
self.all_nodes -= self.visited
print()
if __name__ == '__main__':
g = ProcGraphRecursively()
g.make_graph_from_list(
[[0, 1], [0, 3], [1, 2], [1, 3], [1, 5], [1, 6], [2, 3], [2, 4], [2, 5], [3, 4], [4, 6]]
)
g.depth_first_search()
g = ProcGraphRecursively()
g.make_graph_from_list([[1, 2], [1, 3], [2, 4], [2, 5], [6, 7], [7, 8]])
g.depth_first_search()
class ProcGraphRecursively:
def __init__(self):
self.graph = defaultdict(list)
self.all_nodes: set[int] = set() # disjoint graph 用 (全てのノードを列挙)
def insert_edge(self, v1: int, v2: int):
"""
edge が1つずつ渡される場合に graph に追加する
"""
self.graph[v1].append(v2)
self.all_nodes.add(v1)
self.all_nodes.add(v2)
def make_graph_from_list(self, ad_list: list[list[int]]):
"""
edges が list の list として渡されたときに graph を作成する
param ad_list: [[1, 2], [1, 3], ...]
"""
for v1, v2 in ad_list:
self.graph[v1].append(v2)
self.all_nodes.add(v1)
self.all_nodes.add(v2)
def depth_first_search(self):
def dfs(self, node: int):
if node not in self.visited:
print(node, end=' ')
self.visited.add(node)
for ad_node in self.graph[node]:
dfs(self, ad_node)
while self.all_nodes:
self.visited: set[int] = set()
for start_node in self.all_nodes:
break
dfs(self, start_node)
self.all_nodes -= self.visited
print()
if __name__ == '__main__':
g = ProcGraphRecursively()
g.make_graph_from_list(
[[0, 1], [0, 3], [1, 2], [1, 3], [1, 5], [1, 6], [2, 3], [2, 4], [2, 5], [3, 4], [4, 6]]
)
g.depth_first_search()
# 出力例: 0 1 2 3 4 6 5
g = ProcGraphRecursively()
g.make_graph_from_list([[1, 2], [1, 3], [2, 4], [2, 5], [6, 7], [7, 8]])
g.depth_first_search()
# 出力例: 1 2 4 5 3
# 6 7 8
Complexity Analysis
(アルゴリズム解析)
Time complexity (実行計算時間):
Graph を構成する vertices の数を V、edges の数を E とすると O(V+E) です。
Space complexity (実行メモリ要求量):
Vertices の数分のスタック、disjoint graph にも対処できるようにするための set を利用していますから O(V) です。
DFS Traversal of Trees
(深さ優先探索を利用したツリーの探索)
DFS (Depth First Search) を利用したツリーの探索には、ノードとその子ノードを処理する順番の違いによって3つの方法があります。ノードを N、その左子ノードを L、右子ノードを R とすると、いずれの方法でも L は常に R よりも先に探索されますが、N との探索の順番がそれぞれ異なります:
In-order Traversal (中間探索: L - N - R)
Pre-order Traversal (事前探索: N - L - R)
Post-order Traversal (事後探索: L - R - N)
子ノード L, R に対して N の探索をいつ行うか、によって3つに分かれています。
ツリーに含まれているノードの数が n 個の場合、いずれの方法でも time complexity (実行計算時間) は O(n) です。これは幅優先探索 (BFS: Breath First Search) でも変わりません。
しかし DFS と BFS では space complexity (実行メモリ要求量) が異なります。BFS はツリーの「幅」を問題としますから、将来的に処理すべきノードをセットしておくキュー (queue) の大きさはツリーの最大幅 w に比例します。つまり実行メモリ要求量は O(w) です。一方 DFS はツリーの「高さ」を問題とします。ですから将来的に処理すべきノードをセットしておくスタックの大きさはツリーの最大高 h に比例します。ですから実行メモリ要求量は O(h) となります。
高さが h のバイナリツリーにおける最大幅はルートの高さを 0 とした場合 2ʰ です。また、ノードの配置が左右対称である完全バイナリツリー (complete binary tree) の場合のノードの総数は 2ʰ⁺¹ - 1 になります。
例えば下の図 (a) の完全バイナリツリーで考えてみましょう:
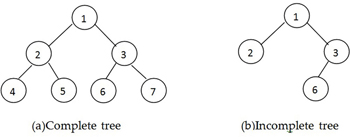
Complete tree (a) と incomplete tree (b) の例
- Shyamkant Limaye (2021). Python Quick Interview Guide. BPB Publications -
このツリーの高さ h は 2 です。また、高さ 2 におけるノードの数は 4 です。この完全バイナリツリーを構成するノードの総数は 1 + 2 + 4 = 7 であり 2²⁺¹ - 1 になっています。つまり完全バイナリツリーにおけるノードの最大値は 2ʰ⁺¹ - 1 ということです。また n 個のノードで構成されるバイナリーツリーの h が取り得る最小値は以下の式で求めることができます:
h = log₂(n+1) - 1 = O(log n)
上の (a) のツリーでは log₂(7+1) - 1 = log₂8 - 1 = 3 - 1 = 2 となります。
逆に n 個のノードで構成されるバイナリツリーの h が取り得る最大値は n - 1 です (ルートノードの h [階層レベル] は 0 であることを忘れないでください)。この場合のバイナリーツリーは全てのノードが1本に繋がった「斜め線」を形成し、各レベル (階層: h) には1つのノードしか含まれていません。つまりこの場合のバイナリツリーの構造は singly-linked list (単方向連結リスト) に類似していることになります。
ツリーの探索にどの方法を採用するか、は、「メモリ要求量」と「探索すべきオブジェクトが存在していそうな場所」から判断することになります。もし探索対象のオブジェクトが「ルート付近」にある可能性が高いのであれば BFS が向いているでしょうし、ツリーの末端近くに存在する可能性が高いのであれば DFS を選択することになるでしょう。
また DFS を用いた横断 (traversal) / 検索 (search) において back edge の存在が確認できれば、その graph には cycle (循環) が存在するということを意味します。つまり、DFS アルゴリズムは「循環の検出」に最適な方法である、ということができます。
Back edge について:
今回の DFS アルゴリズムの実装では "back edge" と言われてもなかなか「ピンッ」と来ないかもしれません。それは、現在対象としているノードとその隣接リストに含まれている子ノード (child node, adjacent node) への edge が back edge であるか否か、の判断が、ただ単にその子ノードが「既に visited リストに含まれているか」だけで決定してしまうからです。
これは今回作成している「隣接リスト」の性格によるものです。今回作成している隣接リストは「単方向」であり「双方向」ではありません。つまりノード 0 の隣接リストは [1, 3] ですが、ノード 1 の隣接リストにはノード 0 を含んでいません。ですから、現在処理中のノードから「既に訪問済みのノード」への edge が見つかった段階で「循環がある」と判断できるわけです。しかしこれだと "back edge" の何たるか、の本質が非常に掴み辛いですね。少し長くなりますが良い機会ですから "back edge" をちゃんと理解しましょう。
Back edge の話を進める前に再確認しておく必要がある事柄について触れておきます。Graph (グラフ) は vertices (nodes: 頂点) と edges (lines: 辺) で構成される non-linear (非線形) な data structure (データ構造) です。その中でも、全ての nodes が「接続されていて (connected)」かつ「循環がない (acyclic)」ものを tree (ツリー) と呼んでいます。
ですから「循環を検出する」ために DFS をツリーに適用する、というのは矛盾がありますから考慮しません。あくまでも「循環が存在する可能性がある」データ構造であるグラフに対して適用して意味を為します。
また、グラフに対して DFS を適用する、ということは「ツリーデータ構造を形成している」ということにほかなりません。つまり明確なルートノード、親ノード、子ノードの区別がないデータ構造であるグラフに対して、あるノードの子ノード、その子ノードの子ノード ... というようにその枝の末端まで辿り、そこで来た道を戻って (backtracking) まだ訪問していないノードが見つかれば再びその枝に入っていき末端まで ... という処理を行っているわけですから。つまりグラフに対して「親ノード」「子ノード」という概念を導入して処理を行なっている、ということです。
ここまで再認識して初めて「DFS における back edge」という考えが理解できるようになります。
グラフに対して DFS を適用することは、「親ノード」「子ノード」という概念を導入する、ということです。子ノードを末端まで辿っていく中で、ある子ノードの隣接リストに含まれる「子ノード」を選択して更にその枝を「深く」進んでいくわけですが、この選択した「子ノード」の実体が「自分の直接の親ノード以外」の「祖先ノード (ancestor node)」であればその edge こそが back edge です。
自分の親ノードと自分が「接続している」のは当たり前ですし、ツリー構造を辿ってきているわけですから自分が処理される時点で、現在処理中の「枝」に属している親ノード、かつ、祖先ノードが「訪問済み (visited)」であることも当然です。ですから、自分の「子ノード」として選択した処理対象のノードが既に visited リストに含まれており、かつ、それが自分の親ノードでなければ、その「子ノード」は「祖先ノード (ancestor node)」のいずれか、ということです。つまり、自分とその「子ノード」を接続している edge は自分の「祖先ノード」への back edge である、ということになります。
ですから本来であれば、DFS における現在処理中の edge が back edge であるか否か、を判断するためには visited リストだけでは不十分で、自分の「親ノードの情報」も必要だ、ということです。しかし今回の例のように「単方向」隣接リストを作成するとこの手間が省ける一方で back edge という概念を理解するのが少し困難になる、ということなんですね。
長々とした説明になりましたがいかがだったでしょうか?同じグラフについて「単方向隣接リスト」と「双方向隣接リスト」を作成し、手書きで DFS の処理の流れを追ってみることをお薦めします。朧げにでも納得出来たような気がすればシメシメです。あとは様々なグラフに対して back edge 情報を出力するように改良を加えたコードを実行し、理解を深めていくだけです。
それぞれのノードがラベル付けされていない (全てのノード間に区別がない) 場合、n 個のノードから作成可能なバイナリツリー (binary tree) の総数は Cn = (2n)! / ((n + 1)!n!) で、n 個のノードをもつ binary search tree の総数と等しくなります。この Cn のことを Catalan number (カタラン数) と呼びます。また、それぞれのノードがラベル付けされている (全てのノードが区別可能な) 場合、ラベル付けされていないそれぞれのパターンにおいてラベルを順列に並べる n! 通りの方法が考えられますから、(2n)! / ((n + 1)!n!) * n! 通りのバイナリツリーが作成可能です。