Python Coding Challenge - How will you find the lowest common ancestor in a binary tree?
(Python コーディングチャレンジ [バイナリツリーを構成する2つのノードに共通する最も身近な親ノードを探そう!] 編)
(Python コーディングチャレンジ [バイナリツリーを構成する2つのノードに共通する最も身近な親ノードを探そう!] 編)
厳格な階層ルールが規定されている会社を想像してください。この会社では部下に指示を出せるのは直属の上司だけです。ですからもし Nana さんが別の部門に所属する同僚の Saki さんに何かを依頼したい場合、彼女はまず直属の上司にその依頼を出し、彼女の上司はそのまた上司に依頼を提出し、...、ということを Saki さんが属する階層の上位に位置する Yuka さんに達するまで行ない、その後 Yuka さんから Saki さんに指示が届くまで階層を下っていくことになります。
このような指示の流れがある度に一旦組織の最上層である CEO まで昇り詰めてから目的の人物まで降りていく、ということは避けたいですから、Nana さんと Saki さんに共通する最も身近な上司を探し当てる必要があります。ここでは問題を単純化するために、1人の上司に所属している部下は2人だけ、ということにします。つまりこの会社の階層構造はバイナリツリー (binary tree) でモデル化できる、ということです。
問題:
ツリーのルートノード root と、そのツリーに含まれている2つのノード p, q の情報が渡されます。この時、ノード p, q に共通する最も身近な親ノードを返すプログラムを記述してください。
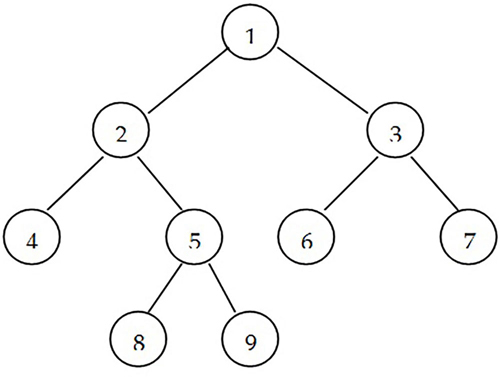
今回の例題、課題で使用するバイナリツリーを表現する隣接リストは [1, 2, 3, 4, 5, 6, 7, None, None, 8, 9, None, None, None, None] となり、これを図で表すと下図のようになります:
NOTE:
例 1:
与えられるパラメータ: root, n8, n6
# 出力: n1
例 1 の解説:
ノード 8 とノード 6 に共通する最も身近な親ノードはノード 1 ですからそれを返します。
例 2:
与えられるパラメータ: root, n4, n9
# 出力: n2
例 2 の解説:
ノード 4 とノード 9 に共通する最も身近な親ノードはノード 2 ですからそれを返します。
また関数定義は以下のような形です (同じである必要はありません):
from typing import Optional, Any
class TreeNode:
"""
binary tree を構成する個々のノード (node) を象徴するクラス
"""
def __init__(self, v: Any):
self.val = v
self.left: Optional['TreeNode'] = None
self.right: Optional['TreeNode'] = None
def lowest_common_ancestor(root: TreeNode, p: TreeNode, q: TreeNode) -> Optional[TreeNode]:
...
class TreeNode:
"""
binary tree を構成する個々のノード (node) を象徴するクラス
"""
def __init__(self, v: Any):
self.val = v
self.left: Optional['TreeNode'] = None
self.right: Optional['TreeNode'] = None
def lowest_common_ancestor(root: TreeNode, p: TreeNode, q: TreeNode) -> Optional[TreeNode]:
...
作成したプログラムは以下のテストをパスする必要があります:
import unittest
class LowestCommonAncestorTest(unittest.TestCase):
def setUp(self):
self.root = self.n1 = TreeNode(1)
self.root.left = self.n2 = TreeNode(2)
self.root.right = self.n3 = TreeNode(3)
self.n2.left = self.n4 = TreeNode(4)
self.n2.right = self.n5 = TreeNode(5)
self.n3.left = self.n6 = TreeNode(6)
self.n3.right = self.n7 = TreeNode(7)
self.n5.left = self.n8 = TreeNode(8)
self.n5.right = self.n9 = TreeNode(9)
def test_1(self):
res = lowest_common_ancestor(self.root, self.n8, self.n6)
self.assertEqual(res, self.n1)
def test_2(self):
res = lowest_common_ancestor(self.root, self.n4, self.n5)
self.assertEqual(res, self.n2)
def test_3(self):
res = lowest_common_ancestor(self.root, self.n6, self.n7)
self.assertEqual(res, self.n3)
def test_4(self):
res = lowest_common_ancestor(self.root, self.n4, self.n9)
self.assertEqual(res, self.n2)
if __name__ == '__main__':
unittest.main()
Level 0: 1
Level 1: 2 3
Level 2: 4 5 6 7
Level 3: None None 8 9 None None None None
class LowestCommonAncestorTest(unittest.TestCase):
def setUp(self):
self.root = self.n1 = TreeNode(1)
self.root.left = self.n2 = TreeNode(2)
self.root.right = self.n3 = TreeNode(3)
self.n2.left = self.n4 = TreeNode(4)
self.n2.right = self.n5 = TreeNode(5)
self.n3.left = self.n6 = TreeNode(6)
self.n3.right = self.n7 = TreeNode(7)
self.n5.left = self.n8 = TreeNode(8)
self.n5.right = self.n9 = TreeNode(9)
def test_1(self):
res = lowest_common_ancestor(self.root, self.n8, self.n6)
self.assertEqual(res, self.n1)
def test_2(self):
res = lowest_common_ancestor(self.root, self.n4, self.n5)
self.assertEqual(res, self.n2)
def test_3(self):
res = lowest_common_ancestor(self.root, self.n6, self.n7)
self.assertEqual(res, self.n3)
def test_4(self):
res = lowest_common_ancestor(self.root, self.n4, self.n9)
self.assertEqual(res, self.n2)
if __name__ == '__main__':
unittest.main()
# テスト用途で作成したバイナリツリーを「グラフ理論の基礎総復習 その3 - ツリーの表現と操作」の回で作成した print_tree() で出力した結果:
Level 0: 1
Level 1: 2 3
Level 2: 4 5 6 7
Level 3: None None 8 9 None None None None
考え方:
もし TreeNode オブジェクトが親ノードへのポインタを保持しているのであれば問題は簡単です。この場合は次の2つのステップで問題は解決します:
ノード p の親ノードを上へ辿りながら全ての親ノードを list / linked list / set / dictionary といったデータ構造に保存していきます。
続いてノード q の親ノードを上へ辿りながら1つ1つの親ノードについてノード p の親ノードデータリストに含まれていないかどうかをチェックします。もし含まれていればそれが探していた「共通する直近の上司」になります。
このような場合、検索速度を上げるためにノード p の親ノードを保存するデータ構造は set を選択した方がよいでしょう。
しかし残念ながら実際の TreeNode オブジェクトには親ノードの情報は保存されていません。ですからこの問題を解決するためにはプログラム内でこのデータ構造を作り上げる必要があります。今回の実装例では子ノードを key、その親ノードを value ペアとする dictionary を組み立てていきます。この辞書 parent の初期値は {root: None} です。ルートノードに親はいませんからね。
操作はルートノードから始めてツリーを走査していきます。そしてそれぞれのノードにおいて、自分の子ノード (left / right) と自分 (親) のペアを作り parent 辞書に保存していきます。また、自分の子ノードに対しても将来的に同様の操作をする必要がありますから、子ノードは「未操作のノード」としてスタックに積むようにします。1回のループ処理ではこのスタックからノードを pop しこの処理を行ないます。このスタックの初期値は root だけです。
ツリーを構成する全てのノードに対してこの処理を行う必要はありません (でも、行う必要がある場合もあるかもしれません)。それは、p と q の2つのノードが見つかればそれ以上の処理をする必要がないからです。この判断をするために2つのフラグ p_not_found と q_not_found を定義し True で初期化しておきます。そして p が見つかれば p_not_found を、q が見つかれば q_not_found を False にします。上記のループ処理はこのどちらかのフラグが True である限り続けることになります。
間違えないでいただきたいのは、このプログラムに渡されてくる全てのパラメータ root, p, q は全て TreeNode オブジェクトであって、ノードオブジェクトの val 値ではありません。「プログラムがパスすべきテスト」で用意しているテストデータや assert 文での検証内容をもう一度確認してください。
プログラム実装例:
from typing import Optional, Any, Optional
class TreeNode:
"""
binary tree を構成する個々のノード (node) を象徴するクラス
"""
def __init__(self, v: Any):
self.val = v
self.left: Optional['TreeNode'] = None
self.right: Optional['TreeNode'] = None
def lowest_common_ancestor(root: TreeNode, p: TreeNode, q: TreeNode) -> Optional[TreeNode]:
stack: list[TreeNode] = [root]
parent: dict[TreeNode, TreeNode] = {root: None}
p_not_found = True
q_not_found = True
while p_not_found or q_not_found:
node = stack.pop()
if node == p:
p_not_found = False
if node == q:
q_not_found = False
if node.left:
parent[node.left] = node
stack.append(node.left)
if node.right:
parent[node.right] = node
stack.append(node.right)
ancestors = set()
while p:
ancestors.add(p)
p = parent[p]
while q not in ancestors:
q = parent[q]
return q
class TreeNode:
"""
binary tree を構成する個々のノード (node) を象徴するクラス
"""
def __init__(self, v: Any):
self.val = v
self.left: Optional['TreeNode'] = None
self.right: Optional['TreeNode'] = None
def lowest_common_ancestor(root: TreeNode, p: TreeNode, q: TreeNode) -> Optional[TreeNode]:
stack: list[TreeNode] = [root]
parent: dict[TreeNode, TreeNode] = {root: None}
p_not_found = True
q_not_found = True
while p_not_found or q_not_found:
node = stack.pop()
if node == p:
p_not_found = False
if node == q:
q_not_found = False
if node.left:
parent[node.left] = node
stack.append(node.left)
if node.right:
parent[node.right] = node
stack.append(node.right)
ancestors = set()
while p:
ancestors.add(p)
p = parent[p]
while q not in ancestors:
q = parent[q]
return q
Complexity Analysis
(アルゴリズム解析)
Time complexity (実行計算時間):
バイナリツリーを構成するノード数を n とすると n 回のループ処理を行なっていますから O(n) です。Dictionary (ハッシュテーブル) の検索は O(1) で行われますから影響ありません。
Space complexity (実行メモリ要求量):
最悪で n 個の要素を含む dictionary と set を作成しています。よって O(2n)、つまり O(n) です。
CHALLENGE:
「グラフ理論の基礎総復習 その3 - ツリーの表現と操作」の回で作成した print_tree() の実装を利用して「バイナリツリーからノードオブジェクトを要素とする隣接リストを作成する」過程で p / q を探し出すという再帰処理で実装する方法もあります。この場合は親ノードを探し出すために各階層のノードで構成されるリストのインデックス番号情報とその受け渡しが必要となります。是非この方法での実装も考えてみてください。
このように色々な方法で graph を扱ううちに苦手意識もなくなりデータを自由に扱えるようになります。リストを受け取ってそれぞれの要素を value とする TreeNode オブジェクトからなるバイナリツリーの作成、バイナリツリーデータの出力、バイナリツリーからそれを表現している隣接リストの作成、と既にこれだけのことができるようになっているはずです。