Python Coding Challenge - How will you select flowers so that the adjacent gardens are not the same?
(Python コーディングチャレンジ [隣り合った庭園には異なる花が植えられているようにするにはどの花を植えればいい?] 編)
(Python コーディングチャレンジ [隣り合った庭園には異なる花が植えられているようにするにはどの花を植えればいい?] 編)
この問題も前回の「噂は本当? Town judge を探せ!」と同様、問題文から如何にグラフ理論に基づいたモデルを導き出せるか、が鍵となります。また、四色定理 (four color theorem) や地図塗りつぶし問題 (map coloring problem) の派生問題と捉えることができる課題です。
問題:
あなたの手元には 1, 2, 3, 4 という4種類の花の種があります。それらを 1 から N までラベル付けされた N 個の庭園に植えようと考えています。
それぞれの庭園は複数の通路で結ばれており [x, y] といった要素からなるリスト paths で表現されます。全ての経路を表す paths リストの1つの要素が [x, y] である場合、x という番号で示される庭園と y という番号で示される庭園の間には互いに行ったり来たりできる双方向の経路 (bidirectional path) が存在する、ということです。また、1つの庭園に繋がる経路は最大で3つあります。
今回花を植えるにあたって庭園技師に相談したところ、経路で結ばれている隣り合った庭園の花は互いに異なるようにした方がよい、というアドバイスをもらいました。
それぞれの庭園に植えるべき花を選択するプログラムを記述してください。このプログラムの返却値は植えるべき花の番号からなるリストです。例えば、answer[i] には (i + 1) 番目の庭園に植えるべき花の番号が入るようにします。
条件を満たす組み合わせは必ず存在します。ただし正解が一意に決まるわけではありません。結果的に庭園技師のアドバイスを満たしていれば正解とします。
例 1:
与えられる入力: N = 4, paths = [[1, 2], [2, 3], [3, 1], [3, 4]]
# 出力: [1, 2, 3, 1]
例 1 の解説:
庭園 1, 2, 3 は「完全に接続 (fully connected)」されていますから 3 種類の異なる花が必要です; 1, 2, 3。庭園 4 は庭園 3 としか接続していませんから庭園 3 に植える花 (3) 以外であれば何でも大丈夫です。
例 2:
与えられる入力: N = 4, paths = [[1, 2], [3, 4]]
# 出力: [1, 2, 1, 2]
例 2 の解説:
庭園 1 と庭園 2 は互いに接続されています。庭園 3 と庭園 4 も互いに接続されています。それ以外の接続は存在しませんから、2種類の異なる花があれば条件を満たすことができます。ですから正解の1つは [1, 2, 1, 2] になります。
例 3:
与えられる入力: N = 4, paths = [[1, 2], [2, 3], [3, 4], [4, 1], [1, 3], [2, 4]]
# 出力: [1, 2, 3, 4]
例 3 の解説:
庭園 1, 2, 3, 4 は「完全に接続 (fully connected)」されています。よって4種類の異なる花が必要です。
NOTE:
Graph において「完全に接続 (fully connected)」されている、ということがどういうことか理解が朧げな場合は「グラフ理論の基礎総復習」を参照してください。
また関数定義は以下のような形です (同じである必要はありません):
def garden_no_adjacent(N: int, paths: list[list[int]]) -> list[int]:
...
...
作成したプログラムは以下のテストをパスする必要があります:
import unittest
class TestGardenNoAdjacent(unittest.TestCase):
def test_1(self):
N = 4
paths = [[1, 2], [2, 3], [3, 4], [1, 3]]
res = garden_no_adjacent(N, paths)
self.assertEqual(res, [1, 2, 3, 1])
def test_2(self):
N = 3
paths = [[1, 2], [2, 3], [3, 1]]
res = garden_no_adjacent(N, paths)
self.assertEqual(res, [1, 2, 3])
def test_3(self):
N = 4
paths = [[1, 2], [3, 4]]
res = garden_no_adjacent(N, paths)
self.assertEqual(res, [1, 2, 1, 2])
def test_4(self):
N = 4
paths = [[1, 2], [2, 3], [3, 4], [4, 1], [1, 3], [2, 4]]
res = garden_no_adjacent(N, paths)
self.assertEqual(res, [1, 2, 3, 4])
def test_5(self):
N = 7
paths = [[1, 2], [2, 3], [2, 4], [5, 6], [6, 7]]
res = garden_no_adjacent(N, paths)
self.assertEqual(res, [1, 2, 1, 1, 1, 2, 1])
def test_6(self):
N = 1
paths = []
res = garden_no_adjacent(N, paths)
self.assertEqual(res, [1])
if __name__ == '__main__':
unittest.main()
class TestGardenNoAdjacent(unittest.TestCase):
def test_1(self):
N = 4
paths = [[1, 2], [2, 3], [3, 4], [1, 3]]
res = garden_no_adjacent(N, paths)
self.assertEqual(res, [1, 2, 3, 1])
def test_2(self):
N = 3
paths = [[1, 2], [2, 3], [3, 1]]
res = garden_no_adjacent(N, paths)
self.assertEqual(res, [1, 2, 3])
def test_3(self):
N = 4
paths = [[1, 2], [3, 4]]
res = garden_no_adjacent(N, paths)
self.assertEqual(res, [1, 2, 1, 2])
def test_4(self):
N = 4
paths = [[1, 2], [2, 3], [3, 4], [4, 1], [1, 3], [2, 4]]
res = garden_no_adjacent(N, paths)
self.assertEqual(res, [1, 2, 3, 4])
def test_5(self):
N = 7
paths = [[1, 2], [2, 3], [2, 4], [5, 6], [6, 7]]
res = garden_no_adjacent(N, paths)
self.assertEqual(res, [1, 2, 1, 1, 1, 2, 1])
def test_6(self):
N = 1
paths = []
res = garden_no_adjacent(N, paths)
self.assertEqual(res, [1])
if __name__ == '__main__':
unittest.main()
考え方:
N 個のノードとノードの接続状況を表す edges の組み合わせリストが与えられますから、この問題は「無向グラフ (undirected graph)」としてモデル化できることが分かります。
例 1 における paths リストが表現している無向グラフを図示してみると下図の (a) になります。またこの図では、4種類の花をそれぞれ (b) のように表した場合の割り当てパターンも併せて表現しています:
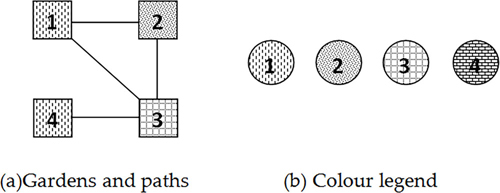
例 1 の paths で表現されるグラフ (a) と割り当てる花の凡例 (b)
- Shyamkant Limaye (2021). Python Quick Interview Guide. BPB Publications -
プログラムでこの割り当てパターンを求めるために、まず「答え」として返すリスト flowers を用意します。このリストの要素数は庭園の数 N と同数にし、「インデックス番号 + 1」が表す庭園にどの花 (1 - 4) が割り当てられているかをセットします。この flowers リストの全ての要素の初期値は 0 です。Python における list は 0 ベースですが庭園番号は 1 から始まっていますから、番号 i の庭園に割り当てられている花を参照するには flowers[i - 1] となりますね。
続いて必要なことは、graph を表現する「隣接リスト (adjacency list)」を作成することです。今回は1つのノードから最大で3本の経路が出ていますから、key を「ノード」、value を「そのノードと接続しているノードのリスト」、として保持する dictionary として実装します。与えられた paths をループしながら情報を追加していくことになりますが、この時まだ dictionary 内に存在しない key に対して接続ノードを append してもエラーが出ないように、通常の dictionary ではなく collections モジュールの defaultdict を利用します。
もし paths の要素が [n1, n2] であれば、node 1 をキーとする value リストに node 2 を追加し、node 2 をキーとする value リストに node 1 を追加していく、ということになります。例えば例 1 の隣接リストは次のようになります:
1: [2, 3]
2: [1, 3]
3: [1, 2, 4]
4: [3]
2: [1, 3]
3: [1, 2, 4]
4: [3]
準備は整いましたからいよいよ各庭園に植えるべき花の割り当て作業に移ります。まず全ての庭園の番号をループするカウンタ i を定義します。つまり i は 1 から N まで動いていきます。1回のループごとに「この庭園に植えることが可能な花」の番号を保持するリスト types を初期化します。今回は花の種類が4種類ですから、このリストの初期値は [1, 2, 3, 4] となります。
NOTE:
要素の検索や削除等の操作の効率を考えた場合、本来は types のデータ型として set を利用した方が良いでしょう。ただしこの課題では答え合わせの手段として unittest の assertEqual 文を利用しており、また、どのような順番で花の割り当てが行われているか、を確認してもらうために「順番」を保持しておく必要があることから、ここでは set ではなく list を利用しています。
取り出した i 番目の庭園に「隣接する (接続している)」庭園のスキャンを行います。ここでは「それらの庭園に既に割り当てられている花番号」を flowers リストを参照して確認し、その花が「この庭園に割り当てることが可能な花番号」リスト types に含まれていれば削除します。この作業によって「隣接する庭園には同じ花を植えない」という庭園技師のアドバイスを実現しているわけです。その作業をすべて終えた後に types リストに残っている花が「この庭園に植えることが可能な花」になります。
今回の実装ではこの時点で types リストに残っている「先頭」の要素を割り当てています。もしこの types のデータ型として set を利用している場合は pop() を使用して任意の要素を取得することになるでしょう。
最終的に flowers リストを返してプログラムを終了します。
プログラム実装例:
from collections import defaultdict
def garden_no_adjacent(N: int, paths: list[list[int]]) -> list[int]:
flowers = [0 for _ in range(N)] # 各庭園に割り当てる花番号 (返却値)
path_graph = defaultdict(list) # paths リストが表現する graph の隣接リスト
for n1, n2 in paths:
path_graph[n1].append(n2)
path_graph[n2].append(n1)
for i in range(1, N + 1):
types = [1, 2, 3, 4] # 割り当て可能な花番号
for neighbor in path_graph[i]: # 接続している庭園で使用している花は除外する
if flowers[neighbor - 1] in types:
types.remove(flowers[neighbor - 1])
flowers[i - 1] = types[0] # 花の割り当て
return flowers
def garden_no_adjacent(N: int, paths: list[list[int]]) -> list[int]:
flowers = [0 for _ in range(N)] # 各庭園に割り当てる花番号 (返却値)
path_graph = defaultdict(list) # paths リストが表現する graph の隣接リスト
for n1, n2 in paths:
path_graph[n1].append(n2)
path_graph[n2].append(n1)
for i in range(1, N + 1):
types = [1, 2, 3, 4] # 割り当て可能な花番号
for neighbor in path_graph[i]: # 接続している庭園で使用している花は除外する
if flowers[neighbor - 1] in types:
types.remove(flowers[neighbor - 1])
flowers[i - 1] = types[0] # 花の割り当て
return flowers
Complexity Analysis
(アルゴリズム解析)
Time complexity (実行計算時間):
与えられる paths リストの要素数を p、庭園の数を n とします。花の種類は 4 で固定です。隣接リストを作成するループは p 回実行されますから計算実行時間は O(p) です。植える花の種類を決めるパートはループのネストになっています。外側のループは庭園の数 n 分だけ実行されます。内側のループはその庭園に隣接する庭園の数だけ実行されますが、今回の問題では最大で 3 と決められていますから、計算実行時間は O(3) -> O(1) です。types リストに対する検索は O(4) ですが、types のデータ型として set を利用すれば O(1) で実行することが可能になります。よってプログラム全体では O(p+n) となります。
Space complexity (実行メモリ要求量):
庭園 n 個分のエントリを含む隣接リストを作成しています。またそれぞれのエントリは最大で 3 個までの要素を含むリストを保持しています。よって O(3n) -> O(n) です。

