RSSフィードを購読
Basics of Graph Theory
(グラフ理論の基礎)
(グラフ理論の基礎)
Graph を対象とする Python coding challenge の前に Graph (グラフ) の基礎について復習しましょう。Python interview でも取り上げられる項目です。
グラフは point (頂点) と２つの points を結ぶ line (辺) で構成されます。
あるグラフが point を１つだけ含み line を一切含まない場合、そのグラフのことを trivial graph と呼びます。また、points は複数含むが line を一切含まない場合は null graph と呼んでいます。
グラフにおいて、points のことは vertexes (vertices) / nodes、lines のことは edges と呼んでいます。
Edges は、単方向 (unidirectional) [すなわち『有向 (directed)』]、もしくは、双方向 (bidirectional) [すなわち『無向 (undirected)』] のどちらかです。また必要に応じて「重み (weight)」と呼ばれるパラメータが付加される場合があります。これは、その edge を通過するための「コスト」を表しています。
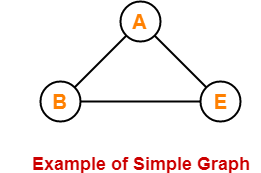
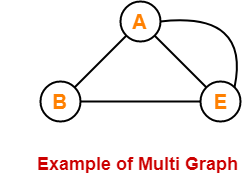
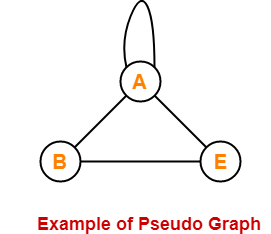
Simple graph は２つの nodes 間を結ぶ edge がただ１つずつだけのもので、それに対して multi graph はある nodes ペアを結ぶ edge が２つ以上あるものを指します。また、pseudo graph はある edge の開始 node と終了 node が同じもの、すなわち、ある node においてループがあるものです。
Simple Graph の例
Multi Graph の例
Pseudo Graph の例
Edges が「無向 (undirected)」である graph は「無向グラフ」と呼ばれています。
無向グラフにおいて、ある vertex に接続している edges の数をその vertex の次数 (degree) といいます。次数が 0 の vertex は「孤立している (isolated vertex)」、次数が 1 の vertex は「ペンダント (pendant vertex)」といいます。グラフが有向である場合は、その vertex に対して入ってくる edge の数 (in-degree: 入次数) と出ていく edge の数 (out-degree: 出次数) を分けて考える必要があります。
グラフ G は G = (V, E) と表されます。ここで、V は頂点 (vetexes) のセット、E は edges のセットです。
無向グラフ (undirected graph) における edges の数は、すべての vertexes の次数の合計の半分に等しくなります。
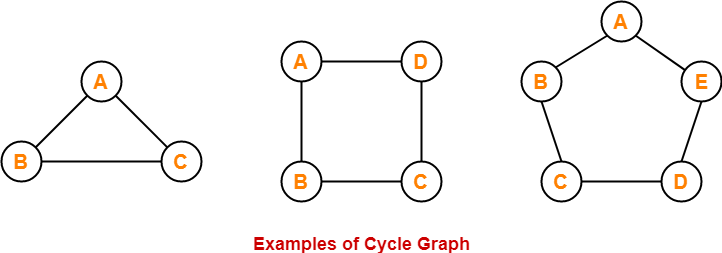
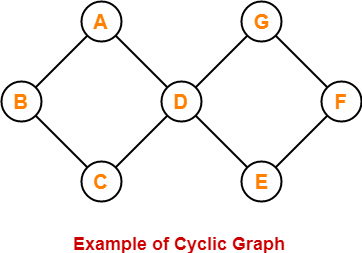
閉路 (cycle) とは、ある vertex から出て結局その同じ vertex に戻ってくる経路 (path) のことを言います。
少なくとも１つの cycle が含まれているグラフは「循環している (cyclic)」と言われます。
Cycle Graph の例
Cyclic Graph の例
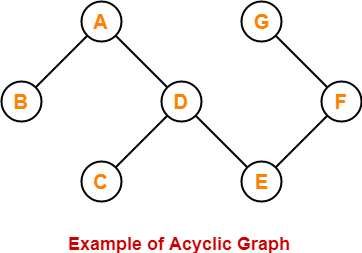
閉路 (cycle) を１つも含まないグラフは 「循環していない (acyclic)」と言われます。
Acyclic Graph の例
ある vertex から他の全ての vertexes へ辿る経路が存在するグラフのことを「接続されている (connected)」と言います。
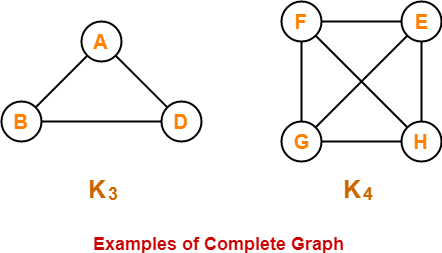
全ての vertices のペア間に edge が存在するグラフを「完全 (complete)」もしくは「完全に接続されている (fully connected)」と言います。このグラフにおける全ての edges の数は、vertices の数を n とすると nC2 = n(n-1)/2 です。
Complete (fully connected) Graph の例
接続されていない vertices のペアが１つでも存在する場合、そのグラフは「非接続 (disconnected)」と言います。
「接続されていて (connected)」かつ「循環していない (acyclic)」グラフは tree です。
「接続されていて循環していない (connected acyclic)」グラフにおける vertices (頂点) と edges (辺) の間には次の関係が成り立ちます: V = E + 1
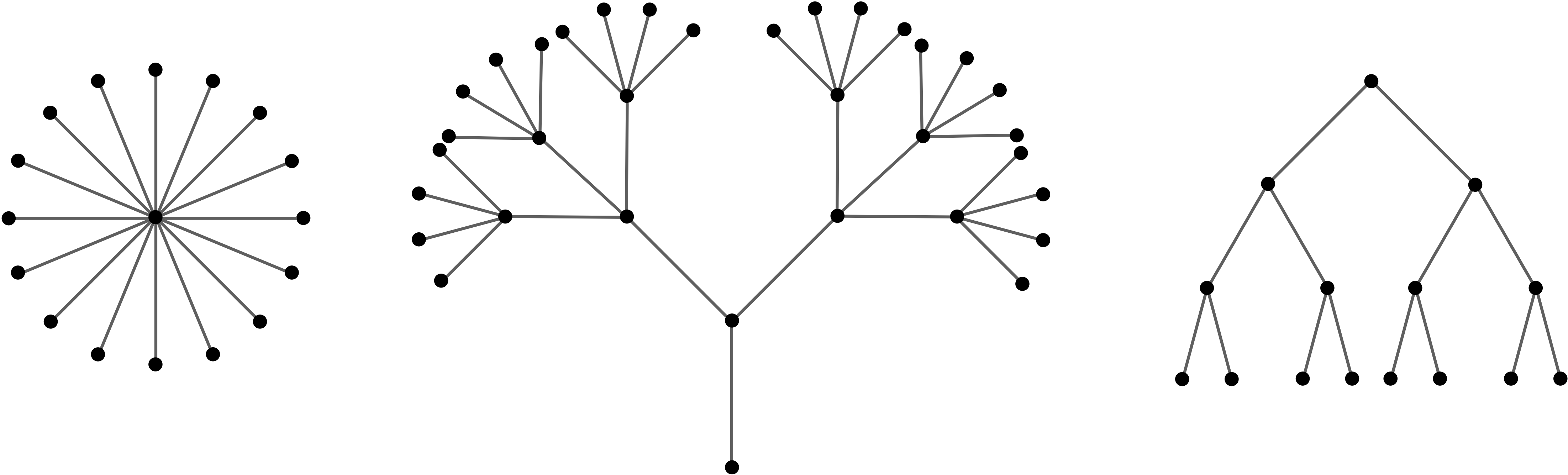
Tree において、１つの node が多くても２つの子ノード (children) までしか持たないものをバイナリツリー (binary tree) と言います。つまり１つの node が持てる子ノードの数は、0, 1, 2 のいずれかです。
Tree を構成する nodes のうち親ノード (parent) を持たないものをルートノード (root node) と言います。
子ノードを持たない node のことをリーフノード (leaf node) と言います。
Forest とは「互いに接続していない (unconnected)」trees の集まりを指します。
Graph における forest の例 (この forest は３つの trees から成り立っている)
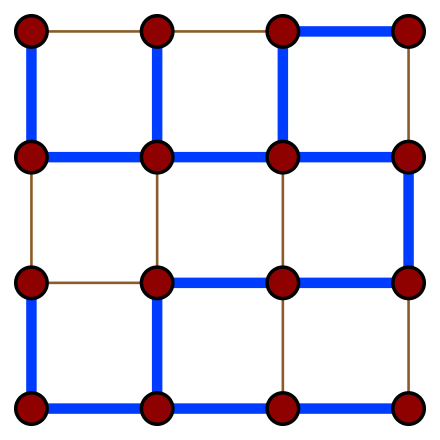
元のグラフ G において、G のすべての頂点 (vertices) を含み、かつ、閉路 (cycle) がなく、かつ、G の一部の辺 (edges) のみを含むサブグラフのことをスパニングツリー (全域木: spanning tree) と言います。下の図では、元のグラフは 4x4 からなるグリッド全体から構成されていますが、その全ての vertices と「青色」の edges からなるサブグラフは spanning tree です。
Spanning tree の例